Tee otsimine kaardil II

80 päevaga ümber maailma rännates oli kaardil tee otsimise programm väga algeline: tee võis läbida sama linna mitu korda, läbitud marsruuti ei salvestatud, suurema linnade arvu korral läheb sealesitatud programm kergesti "umbe", s.t. tuleb Prologi veateade "Stack overflow"). Kuna sarnased otsimisülesanded esinevad praktikas väga sageli, on siin toodud efektiivsem kaardil tee otsimise meetod (seegi ei ole veel parim!). Olgu algandmeteks mõnede Eesti linnade vahelised kaugused.

tee(tallinn, rakvere,97).
tee(rakvere, kohtla_järve,73).
tee(kohtla_järve, narva,50).
tee(kohtla_järve, jõhvi, 11).
tee(tallinn, paide, 97).
tee(paide, tapa, 49).
tee(paide, rapla, 50).
tee(tapa, rakvere, 28).
tee(rakvere, jõgeva, 72).
tee(paide, põltsamaa, 39).
tee(põltsamaa, tartu, 60).
tee(põltsamaa, jõgeva, 27).
tee(jõgeva, mustvee, 40).
tee(mustvee, narva, 122).
tee(kohtla_järve, mustvee, 76).
tee(jõhvi, mustvee, 74).

Kahe linna vahel tee otsimise predikaati matk(Linn1, Linn2, Teepikkus, Linnad) võib kasutada ka kahe linna vahelise lühima tee pikkuse leidmiseks nn "jõumeetodil". Selleks muudame predikaadi matk esimest lauset, asendades seal matka esitamise ekraanil uue lause reis(Teepikkus) lisamisega programmi - nii salvestatakse iga reisi pikkus ja läbitud linnad:

Kuna reis on predikaadiga assert muudetav ühekohaline (ühe argumendiga) predikaat, peaks nüüd ka (programmi algusesse) lisama lause:

Kahe linna vahelise lühima tee pikkuse leidmiseks kogutakse kõigi erinevate reiside pikkused üheks nimistuks ja kasutada siis lyhim kõigi teepikkuste seas minimaalse leidmiseks; predikaat lyhim on täiesti analoogiline nimistus minimaalse/maksimaalse elemendi leidmise predikaadiga, kuid selle argumendiks on mitte nimistu arvudest, vaid kaheelemendilistest nimistustest, kus esimene on arv; tulemus (lühim reis) saadakse samuti kaheelemendilise nimistuna [Pikkus, Läbitud_linnad] :

lyhim(Linn1, Linn2, Lyhim_tee):-
retractall(reis(_)),
otsi(Linn1, Linn2),
findall(Teepikkus, reis(Teepikkus), Teepikkused),
lyhim(Teepikkused, Lyhim_tee).

lyhim[Pikkus], Pikkus):- %kui on vaid üks tee, siis see ongi minimaalne ja edasi pole tarvis otsida
!.

lyhim([Pikkus|Teed], Pikkus):-
lyhim(Teed,Pikkus1),
Pikkus < Pikkus1, !. % esimese tee pikkus on lühem kui järgnevate miinimum, edasi pole enam vaja otsida

lyhim([_|Teed], Pikkus):-
lyhim(Teed, Pikkus). % eelmise lause lõpus oleva ! tõttu kasutatakse seda lauset vaid siis,
% kui esimese tee pikkus ei ole väiksem kui järgnevate miinimum, s.t. järgnevate miinimum ongi lühim tee

Swi-Prologis on ka lihtsam võimalus lühima tee leidmiseks (see ei järgi Prolog-i standardi, s.t. ei tarvitse toimida teistes Prologi interpretaatorites/kompilaatorites). Kui kõik leitud reiside piikused (salvestatud predikaadiga reis(Teepikkus)) koguda süsteemipredikaadiga setof üheks nimistuks, siis setof ka järjestab selle nimistu, seega selle nimistu esimene element esitabki lühimat teed:

Läbitud linnade meelespidamiseks (predikaadis matk nimistu Läbitud asemel) ei saa kasutada linnade salvestamist predikaadiga assert, sest tagurdamise (backtracking-u) korral kord assert-iga salvestatud lauseid ei muudeta (seda on lihtne kontrollida Prologi käsurealt: assert(reis),fail. järel listing(reis) näitab, et lause reis on Prologil alles); assert-i võib kasutada vaid sellise informatsiooni salvestamiseks/meelespidamiseks, mis ülesande lahendamise käigus ei muutu (näiteks mingi linnadevahelise tee salvestamiseks predikaadiga reis).

Väga efektiivse lühima tee algoritmi esitas tuntud hollandi arvutiteadlane Dijkstra. Tema algoritm leiab antud tipust minimaalsed teed korraga kõigisse teistesse tippudesse - osutub, et arvutuste keerukus sellega ei kasva!

Dijkstra algoritmis on graafi tipud jagatud kahte hulka: juba uuritud tipud, mille jaoks on teada lühim tee alguspunktist (läbi seniuuritud tippude) ja veel uurimata tipud. Igal sammul valitakse mingi uuritud tipp ja leitakse selle naabrus, s.t. tipud, kuhu sealt pääseb. Iga sellise tipu jaoks leitakse kaugus (läbi valitud uuritud tipu) algustipust; kui selle tipu jaoks ei olnud seni üldse veel lühima tee hinnangut, lisatakse tipp koos leitud teepikkusega uuritud tippudele; kui kui tippu jaoks oli uuritud uuritud tippude hulgas juba olemas lühim tee, kuid see oli pikem kui praegu leitu, asendatakse see teepikkus äsjaleituga; kui varem leitud tee oli lühem, siis leitud tee unustatakse. Näiteks Tallinnast teistesse linnadesse lühimate teede otsingul muutuvad uuritud ja uurimata linnade nimistud järgmiselt (kasutades tähistust Linn-tee):

min_dist(Start,MinDist):-
dijkstra([],[Start-0],MinDist).

dijkstra(MinDist,[],MinDist).
dijkstra(Uuritud,Uurimata,MinDist):-
vali(Uurimata,V-D,Ylejäänud),
naabrus(V,Naabrus), % Naabrus on nimistu naaberlinnadest koos teepikkustega
diff(Naabrus,Uuritud,UusNaabrus),
merge(UusNaabrus,Ylejäänud,D,UusUurimata),
dijkstra([V-D|Uuritud],UusUurimata,MinDist).

vali([H|T],MinV,Muud):-% vali(+Uurimata,-Uuritav,-MuudUurimata)
vali_lähim(T,H,MinV,Muud).
vali_lähim([],MinV,MinV,[]).
vali_lähim([V1-D1|T],V-D,MinV,[H2|Muud]):-
(D1<D ,!, NextM=V1-D1,H2=V-D;
NextM=V-D,H2=V1-D1),
vali_lähim(T,NextM,MinV,Muud).

diff([],_,[]).% diff(+Tipud,+Uuritud,-Uurimata)
diff([V-D|T],Uuritud,L):-
(member(V-_,Uuritud),!, L=NewT ;
L=[V-D|NewT]), diff(T,Uuritud,NewT).

merge([],L,_,L).% merge(+Tipud,+VanadUurimata,-KõikUurimata)
merge([V1-D1|T],Uurimata,D,UusUurimata):-
(remove(Uurimata,V1-D2,Ylejäänud),!,
VD is min(D2,D+D1);
Ylejäänud=Uurimata,VD is D+D1),
UusUurimata=[V1-VD|Muud],
merge(T,Ylejäänud,D,Muud).

remove([H|T],H,T).
remove([H|T],X,[H|NT]):-
H\=X,
remove(T,X,NT).

1. Lühimat teed arvutav predikaat ei näita, kus reis kulges (millised linnad läbiti). Koosta predikaat linnadevahelise lühima tee esitamiseks. Selleks on mitu võimalust:
lauses otsi meeles pidada ka läbitud linnade nimistu lausega assert(reis(Linn1, Linn2, Teepikkus, Linnad)), koguda siis lausega findall([Teepikkus, Linnad], reis(Linn1, Linn2, Teepikkus, Linnad), Teed) üheks nimistuks kõik paarid (kaheelemendilised alamnimistud) [Teepikkus, Linnad] ja täiendada predikaati lyhim nii, et see leiaks kõigi selliste kaheelemendiliste nimistute nimistus selle, mille esimene element on minimaalne;
lisada fakt reis(Linn1, Linn2, Teepikkus, Linnad) ainult sel juhul, kui kas ühtegi sellist fakti veel ei ole (see on esimene) või äsjaarvutaud reisi pikkus on väiksem kui salvestatud faktis reis(Linn1, Linn2, Teepikkus, Linnad) esinev; sellisel juhul kustutatakse enne salvestatud fakt reis(Linn1, Linn2, Teepikkus, Linnad) ja salvestatakse siis uus, kus on praegu leitud reisi andmed (siis on salvestatud faktis alati kirjeldatud seni leitud reisidest lühim) ja kui predikaat otsi lõpetab töö (predikaadi teises lauses) väljastatakse selle lühima reisi teepikkus ja marsruut.

2. Et muuta tee otsimine sihikindlamaks, võib linnade nimistule lisada ka suunad:

tee(tallinn, rakvere,97,ida,lõuna).
tee(rakvere, kohtla_järve,73,ida,*).
tee(kohtla_järve, narva,50,ida,*).
tee(tallinn, paide, 97,ida,lõuna).
tee(paide, tapa, 49,ida,*).
tee(tapa, rakvere, 28, ida,*).
tee(rakvere, jõgeva, 72, *,lõuna).
tee(paide, põltsamaa, 39, *,lõuna).
tee(põltsamaa, tartu, 60, *,lõuna).
tee(põltsamaa, jõgeva, 27,ida,*).
tee(jõgeva, mustvee, 40,ida, põhi).
tee(kohtla_järve, mustvee, 76, ida,*).
tee(jõgeva, mustvee, 40,ida,põhi).

(siin "*" tähendab, et see suund ei ole oluline, linnad asuvad enam-vähem samal pikkus- või laiuskraadil). Täiendage otsimispredikaati nii, et kunagi ei liigutaks lähtepunkti ja sihtpunkti vahelisele suunale vastupidises suunas. Selleks antakse predikaadile otsi ka sihtlinna suund (näiteks otsi(tallinn, tartu, ida,lõuna) ja täiendatakse predikaati matk nii, et kusagil ei kasutataks suunda, mis on otsitud linna suunale otse vastupidine, s.t. Tallinnast Tartusse teed otsides ei või kasutada teed, mille suunad on "lääs,põhi"; kui antud/teada on vaid yks suund (näiteks otsi(tallinn, narva, ida,*) ), ei või liikuda sellega vastupidises suunas (läände). Loomulikult tuleb määrata ka ilmasuundade vahelised suhted, s.t. et lääs ja ida on vastupidised (seda on tarvis juba predikaadi pääseb kirjelduses).

3. Veel lihtsam kui lühima tee leidmine on graafi kattepuu leidmine. Kattepuu on antud graafi kaartest koostatud tsükliteta graaf, mis ühendab kõikki tippe (s.t. ükskõik millise kaare lisamisel tekiks tsükkel) ja mille kaarte pikkuste kogusumma on minimaalne; selle leidmiseks alustatakse tühja kaarte hulgaga ja valitakse igal sammul veel kasutamata kaarte hulgast minimaalse pikkusega kaar, mis koos juba valitud kaartega ei tekitaks tsüklit. Koosta predikaat kattepuu leidmiseks; selle abil saab näidata, et Eesti raudteevõrk on just selline graaf - minimaalse kogupikkusega, kuid ühendab kõiki (tähtsamaid) linnu.

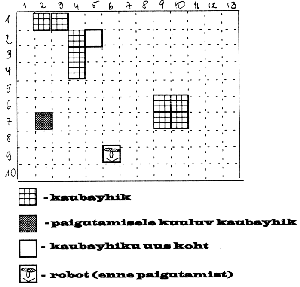
Teha programm laos kaupu ümber paigutava roboti liikumistee arvutamiseks.
Antud on lao mõõtmed n,m; robot liigub mööda ruute (1,1), (2,2),...,(n,m) ja iga kaubaühik katab igal hetkel täpselt ühe ruudu. Antud on paigutamisele kuuluva kauba praegune asukoht (n1,m1), selle sihtkoht (n2,m2) ja laos olevate kaupade asukohad (s1,t1),(s2,t2),..., (sk,tk). Paigutamiseks võtab robot kauba sülle (astub paigutatava kauba ruudule) ja liigub siis sihtruudule; robot ei või astuda kaubale, mida ta praegu ei paiguta (s.t. laos olevatele teistele kaupadele).
Veidi raskemad versioonid:
- robot peab paigutama mitu kaupa (antakse paigutatavate ja sihtkohtade nimistud);
- robot peab ise otsima vabad ruudud (sihtkohad) ja paigutama mitu kaupa nii, et lattu mahuks maksimaalne kaubakogus.

Tee otsimine kaardil ja Dijkstra algoritm