Lõpprekursioon ja keerukus

Kui rekursiivne avaldis sisaldab mitut (varemarvutatud) avaldist, peab lõpprekursiivse programmi saamiseks "kaasa vedama" mitut seniarvutatud jadaliiget ja lõpprekursiivse programmi saamine võib tunduda liiga komplitseerituna, et sellega üldse jännata.

Vaatleme näitena Fibonacci arve. Itaalia linna Pisa matemaatik Leonardo Fibonacci uuris oma aastal 1200 ilmunud raamatus "Liber Abaci" ("Raamat Arvelauast") järgmist probleemi:

Kui iga vähemalt 1 kuu vana paar küülikuid "toodab" järgmise kuu lõpuks uue paari küülikuid ja meil on algul vaid üks paar vastsündinud küülikuid, siis kui palju paare on meil poole aasta, aasta või kahe aasta pärast (eeldades, et kõik küülikud on surematud)?

Kui N-dal kuul on K(N) paari küülikuid, siis järgmise kuu lõpul on alles need K(N) paari. Kuna eelmise kuu lõpul olemas olnud K(N-1) paari on kõik juba rohkem kui 1 kuu vanad ja paljunevad, siis
K(N+1) = K(N) + K(N-1)
Eelmisel kuul sündinud K(N)-K(N-1) paari järgmisel kuul veel ei paljune; tulemusena saame nn Fibonacci rea:
1,1,2,3,5,8,11,...
kus iga järgmine liige on kahe eelmise liikme summa. Selle rea liikemete arvutamine Prologi predikaadina on täiesti analoogiline faktoriaali arvutamisega, kuid ühe funktsiooni K(N) väärtuse asemel peetakse meeles kogu rida K(0), K(1), K(2),...:

fibonacci_jada(0,[1]) :-
!.

fibonacci_jada(1,[1,1]) :-
!.

fibonacci_jada(N,[P,P1,P2|Muud]) :-
N1 is N - 1,
fibonacci_jada(N1,[P1,P2|Muud]),
P is P1 + P2.

Kui see predikaat ei ole lõpprekursiivne. Laseme Prologil endal arvutada, mitu alamülesannet fibonacci_jada ta päringu fibonacci_jada(N,F) täimisel käivitab:

alamylesandeid(0,1) :-
!.

alamylesandeid(1,1) :-
!.

alamylesandeid(N,Ylesandeid) :-
N1 is N - 1,
N2 is N - 2,
alamylesandeid(N1,Ylesandeid1),
alamylesandeid(N2,Ylesandeid2),
Ylesandeid is Ylesandeid1 + Ylesandeid2 + 1.

Et hinnata alamülesannete arvu kasvu, teeme mõne päringu:

?- alamylesandeid(10,N).
N = 177

?- alamylesandeid(20,N).
N = 21891

?- alamülesandeid(30,N).
N = 2692537 ;

ja päringule

?- alamylesandeid(50,N).

tuli 15 minuti pärast vastus:

Local stack full

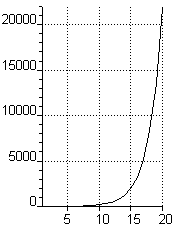
Et paremini aru saada, kuidas alamülesannete arv kasvab, on kõrval lastud Prologil välja joonestada selle funktsiooni graafik (vastavat programmi on selgitatud SWI-Prologi graafikalaiendust XPCE käsitlevas osas); on selge, et see funktsioon kasvab eksponentsiaalselt, s.t. selliselt programmeeritud Fibonacci arvude arvutamise programm kõlbab vaid väga väikeste argumendi N väärtuste korral.
Fibonacci arvude lõpprekursiivse programmi saame, kui peame meeles (näiteks nimistuna) kaks viimast Fibonacci arvu:

fibonacci_arv(0,1):-!.
fibonacci_arv(N,F):-
fibonacci_jada1(1,N,[1,1],[F|_]).

fibonacci_jada1(N,N,L,L):-!.

fibonacci_jada1(N1,N,[F1,F],L):-
N2 is N1+1,
F2 is F1+F,
fibonacci_jada1(N2,N,[F2,F1],L).

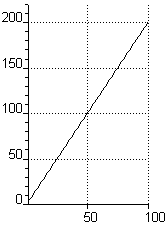Nüüd kasvab alamülesannete arv lineaarselt: N ühe võrra suurendades lisandub vaid kaks arvutusoperatsiooni:

alamylesandeid1(0,1):-!.

alamylesandeid1(N,Y):-
N1 is N-1, alamylesandeid1(N1,Y1),
Y is Y1 + 2.

?- alamylesandeid1(20,Y)

Y = 41

?- alamylesandeid1(100,Y)

Y = 201

Alamülesannete arvu täpne hindamine on sageli raske (kas nimistu esitamine [Pea|Keha] notatsioonis on alamülesanne?). Swi-Prologis on olemas sisseehitatud protseduur time(Eesmärk), mis väljastab Eesmärgi tõestamiseks kulunud aja ja selle aja jooksul Prologi järeldusmehhanismi poolt tehtud sammude arvu.
Vaatleme näitena nimistu tagurpidi pööramist. Naiivne ettekujutus selle ülesande sooritamiseks vajalikust predikaadist on tavaliselt selline: pöörame nimistu Keha tagurpidi ja siis liidame selle lõppu nimistu Pea, s.t. üheelemendilise nimistu, mis koosneb nimistu Pea-st:

nreverse([X|L0],L) :-
nreverse(L0,L1),
concatenate(L1,[X],L).

nreverse([],[]).

concatenate([X|L1],L2,[X|L3]) :-
concatenate(L1,L2,L3).
concatenate([],L,L).

Predikaat nreverse pole lõpprekursiivne. Tegelikult on nimistu tagurpidi pööramine väga lihtne lõpprekursiivne ülesanne: kui järjest tõsta esialgse nimistu esimene element teise nimistu (mis alguses on tühi) algusesse, siis viimasena tõstetakse esimese nimistu viimane element, s.t. tulemuseks saamegi esialgse nimistu tagurpidi kujul:

pööra([E|L1],L2,L):-
pööra(L1,[E|L2],L).

pööra([], L,L).

Nende algoritmide hindamiseks genereerime algul predikaadi integers(N,NL) abil nimistu, mis koosneb kõigist täisarvudest 1..N ja hindame siis mõlema algoritmi nimistu NL tagurpidi pööramisel tehtud järelduste arvu:

integers(N,NL):-
integers(1,N,NL).

integers(Low, High, [Low | Rest]) :-
Low =< High, !,
M is Low+1,
integers(M, High, Rest).

integers(_,_,[]).

test1(N) :-
integers(N,L),
nreverse(L,X).

test2(N):-
integers(N,L),
reverse1(L,[],TL).

?- time(test1(200)).
% 20,906 inferences, 0.01 CPU in 0.01 seconds (100% CPU, 2087594 Lips)

?- time(test2(200)).
% 806 inferences, 0.00 CPU in 0.00 seconds (?% CPU, Infinite Lips)

- lõpprekursiivse meetodi kasutamisel tegi Prolog peaaegu kaks pool korda vähem tööd !

Ülesandeid:

1. Fibonacci jada tüüpi rekursiivselt määratud jadasid kasutatakse sageli nn pseudojuhuslike arvude saamiseks (arvuti on deterministlik ja siin täiesti juhuslikke arve pole võimalik saada); sageli kasutatakse näiteks jadasid
X(N) = X(N-17) + X(N-5) (mod 2**31)
(selle jada periood on 2**47). Tee programm selliste pseudojuhuslike arvude arvutamiseks (loomulikult peab arvud X(0),X(1),...,X(16) ette andma, kuid need võib valida vabalt, kui vad vaid ei ole kõik samad).

Küsimused, probleemid: