
 Kuidas
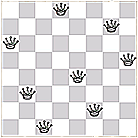
paigutada malelauale kaheksa lippu nii, et nad ei tulistaks (lipud tulistavad
mööda ridu, veerge ja diagonaale) üksteist ?
Kuidas
paigutada malelauale kaheksa lippu nii, et nad ei tulistaks (lipud tulistavad
mööda ridu, veerge ja diagonaale) üksteist ?kombineeri([X1|X],[Y1|Y],[S1|S],[D1|D]) :-
S1 is X1 +Y1,
D1 is X1 - Y1,
kombineeri(X,Y,S,D).
kombineeri([],[],[],[]).
erinevad([X|Y]) :-
not(member(X,Y)), erinevad(Y).
erinevad([X]).
perm([X|Y],Z) :-
perm(Y,W), lisa(X,W,Z).
perm([],[]).
lisa(X,R,[X|R]).
lisa(X,[F|S],[F|R]) :-
lisa(X,S,R).
 ©2004
Jaak Henno
©2004
Jaak Henno