
 Trükiplaatide projekteerimisel on tarvis lahendada
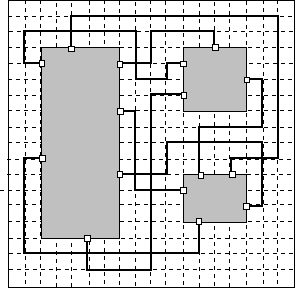
järgmine probleem (routing problem): n x n tasapinnalisel võrestikul on antud m sisendit ja väljundit,
mis on tarvis paarikaupa ühendada nii, et kõik ühendusteed kulgevad mööda võrestiku servi ja samal lõigul
ei kulge kusagil kaks ühendusteed; ühendusteed võivad ristuda, kuid üheski punktis ei või ristuda rohkem
kui kaks teed; sageli nõutakse ka ristumiste koguarvu
minimaliseerimist. Ülesanne sarnaneb kaardil tee otsimise ülesandega: võrestiku servad on otseteed, sisend - lähtelinn ja väljund - sihtpunkt.
Trükiplaatide projekteerimisel on tarvis lahendada
järgmine probleem (routing problem): n x n tasapinnalisel võrestikul on antud m sisendit ja väljundit,
mis on tarvis paarikaupa ühendada nii, et kõik ühendusteed kulgevad mööda võrestiku servi ja samal lõigul
ei kulge kusagil kaks ühendusteed; ühendusteed võivad ristuda, kuid üheski punktis ei või ristuda rohkem
kui kaks teed; sageli nõutakse ka ristumiste koguarvu
minimaliseerimist. Ülesanne sarnaneb kaardil tee otsimise ülesandega: võrestiku servad on otseteed, sisend - lähtelinn ja väljund - sihtpunkt. Järgnevas vaatleme programmi, mis lahendab selle ülesande lihtsustatud variandi: kõik sisendid ja kõik väljundid asuvad samas veerus (seega piisab nende esitamiseks vastava rea numbri andmisest; ühendada tuleb esimene sisend esimese väljundiga, teine sisend teise väljundiga jne. Peale sisendite ja väljundite reanumbreid (need sisestatakse ühekaupa, kui kõik numbrid on sisestatud, sisestatakse sõna 'kõik') on programmi sisendiks veel skeemi laius, st. veergude arv. skeemi ridade arvuks arvutatakse maksimum sisendite ja väljundite reanumbritest.
 Uue tee leiab (st. ühendab ühe sisendi ja sellele vastava väljundi) predikaat
tee (see on väga sarnane kahe linna vahelise
tee leidmise predikaadiga). Selle esimene argument on punkt, kus ollakse praegu, teine -
kuhu on tarvis jõuda, kolmas - nimistu võrgu tippudest, mis on juba läbitud, neljas argument on
vajalik vaid lõpliku tee väljastamiseks ja viies argument on teiste seni juba leitud teede
nimistu (seda vajatakse kontrollimiseks, et sama serva ei kasutata kaht korda).
Punktide [X,Y] ja [X1,Y1]
vahelist teed [X,Y,X1,Y1] (serva) valides püütakse algul liikuda vertikaalsuunas
õigele (s.t. sihtpunkti) kõrgusele ja siis jätkata horisontaalsuunas
Näiteks ülaloleval joonisel sisend [5,1] ja väljund [2,5]
on ühendatud just nii (teede leidmine algab viimasena sisestatud punktist). Kui kohe õigele
horisontaalreale jõudmine not õnnestu, liigutakse üks samm paremale ja proovitakse uuesti.
Kõrvaloleval näitel on punktide [4,1] ja [1,5] ühendamisel Prolog olnud
sunnitud tagurdama ja muutma algul leitud ühendusteed [[4,1],[4,2],[3,2],[2,2],[1,2],[1,3],[1,4],[1,5]],
kui punkte [1,1],[4,5] ühendada püudes selgus, et see tee suleb edasipääsud punktist [1,1]. Abipredikaat kasutatud/3 (s.t. kolme argumendiga - erineva argumentide arvuga predikaadid on Prologis erinevad!) kontrollib, kas kaar (serv) esineb juba mingil teel (servade nimistu, kasutatud/3 teine argument), või teede nimistus (kasutatud/3 kolmas argument) esineval teel, käivitades vastavalt abipredikaadid kasutatud/2 ja kusagil/2. Abipredikaat kasutatud/2 kontrollib, kas kaar või vastassuunaline kaar esineb teel (kaarte nimistu) ja käivitab selleks abipredikaadi esineb. Abipredikaat kusagil/2 kontrollib, kas kaar esineb teede nimistus; selleks käivitab ta (selle kaarega) iga nimistus esineva tee jaoks abipredikaadi kasutatud/2. Abipredikaat esineb kontrollib, kas kaar (nelik [X,Y,X1,Y1]) esineb mingil teel (selliste nelikute nimistu.
Uue tee leiab (st. ühendab ühe sisendi ja sellele vastava väljundi) predikaat
tee (see on väga sarnane kahe linna vahelise
tee leidmise predikaadiga). Selle esimene argument on punkt, kus ollakse praegu, teine -
kuhu on tarvis jõuda, kolmas - nimistu võrgu tippudest, mis on juba läbitud, neljas argument on
vajalik vaid lõpliku tee väljastamiseks ja viies argument on teiste seni juba leitud teede
nimistu (seda vajatakse kontrollimiseks, et sama serva ei kasutata kaht korda).
Punktide [X,Y] ja [X1,Y1]
vahelist teed [X,Y,X1,Y1] (serva) valides püütakse algul liikuda vertikaalsuunas
õigele (s.t. sihtpunkti) kõrgusele ja siis jätkata horisontaalsuunas
Näiteks ülaloleval joonisel sisend [5,1] ja väljund [2,5]
on ühendatud just nii (teede leidmine algab viimasena sisestatud punktist). Kui kohe õigele
horisontaalreale jõudmine not õnnestu, liigutakse üks samm paremale ja proovitakse uuesti.
Kõrvaloleval näitel on punktide [4,1] ja [1,5] ühendamisel Prolog olnud
sunnitud tagurdama ja muutma algul leitud ühendusteed [[4,1],[4,2],[3,2],[2,2],[1,2],[1,3],[1,4],[1,5]],
kui punkte [1,1],[4,5] ühendada püudes selgus, et see tee suleb edasipääsud punktist [1,1]. Abipredikaat kasutatud/3 (s.t. kolme argumendiga - erineva argumentide arvuga predikaadid on Prologis erinevad!) kontrollib, kas kaar (serv) esineb juba mingil teel (servade nimistu, kasutatud/3 teine argument), või teede nimistus (kasutatud/3 kolmas argument) esineval teel, käivitades vastavalt abipredikaadid kasutatud/2 ja kusagil/2. Abipredikaat kasutatud/2 kontrollib, kas kaar või vastassuunaline kaar esineb teel (kaarte nimistu) ja käivitab selleks abipredikaadi esineb. Abipredikaat kusagil/2 kontrollib, kas kaar esineb teede nimistus; selleks käivitab ta (selle kaarega) iga nimistus esineva tee jaoks abipredikaadi kasutatud/2. Abipredikaat esineb kontrollib, kas kaar (nelik [X,Y,X1,Y1]) esineb mingil teel (selliste nelikute nimistu.
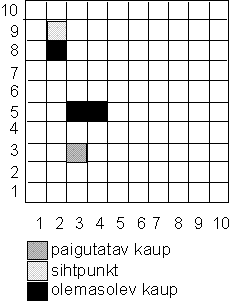 Tee programm laos kaupu ümber paigutava roboti liikumistee arvutamiseseks.
Antud on lao mõõtmed n,m; robot liigub mööda ruute (1,1), (2,2),...,(n,m). Iga kaubaühik katab igal hetkel täpselt ühe ruudu tipu. Antud on paigutamisele kuuluva kauba praegune asukoht (n1,m1) ja selle sihtkoht (n2,m2); ka juba laos olevate kaupade asukohad (s1,t1),(s2,t2),...,(sk,tk). Paigutamiseks võtab robot kauba sülle (astub paigutatava kauba ruudule) ja liigub siis sihtruudule; robot ei või astuda kaubale, mida ta praegu ei paiguta.
Veidi raskem versioon: robot paigutab järjest kuitahes mitu kaubaühikut.
Tee programm laos kaupu ümber paigutava roboti liikumistee arvutamiseseks.
Antud on lao mõõtmed n,m; robot liigub mööda ruute (1,1), (2,2),...,(n,m). Iga kaubaühik katab igal hetkel täpselt ühe ruudu tipu. Antud on paigutamisele kuuluva kauba praegune asukoht (n1,m1) ja selle sihtkoht (n2,m2); ka juba laos olevate kaupade asukohad (s1,t1),(s2,t2),...,(sk,tk). Paigutamiseks võtab robot kauba sülle (astub paigutatava kauba ruudule) ja liigub siis sihtruudule; robot ei või astuda kaubale, mida ta praegu ei paiguta.
Veidi raskem versioon: robot paigutab järjest kuitahes mitu kaubaühikut.
 ©2004
Jaak Henno
©2004
Jaak Henno