NUT

Eelmises peatükis loodud ilmutamata võrrandeid lahendava predikaadi abil on lihtne modellerida Küberneetika Instituudis prohfessor Enn Tõugu juhtimisel loodud tehisintellektisüsteemi NUT.

NUT on inseneriarvutuste lihtsustamiseks. Inseneride põhitöö mingi uue toote, konstruktsiooni loomisel sarnaneb matemaatikaülesande lahendamisele: tuleb kasutatavate objektide omadusi kasutades arvutada ülesande püstituses (spetsifikatsioonis) antud suuruste abil kõik konstruktsiooni parameetrid. Selleks tuleb lähdudes antud suurustest (lähteparameetrid, mille väärtused on antud ülesande püstituses) samm-sammult otsida sobiv võrrand (protseduur, alamprogramm), mille abil saab arvutada mõne uue ülesande lahendamiseks vajaliku suuruse ja jatkata kuni kõik otsitavad suurused on arvutatud. Ülesanne on analoogiline keemiliste reaktsioonide abil mingite uute aintete sünteesimise ülesandega - olemasolevad või juba sünteesitud abiained on suurused, mille väärtus on juba teada, igal sammul tuleb leida sobiv reaktsioon/võrrand uute ainte/suuruste saamiseks ja jätkata seni, kuni on saadud kõik otsitavad ained/suurused; seega kuulub ka see ülesanne kaardil (mitmealuselisel graafil) tee otsimise ülesannete klassi.

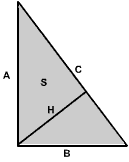Süsteemi töö põhineb teadmistel kasutatavate objektide omadustest; objektide omadusi kirjeldatakse mudelitega, mis kirjeldavad objekti parameetrite (objektis esinevate suuruste) vahelisi seoseid. Näiteks täisnurkse kolmnurga parameetreid: kaatetid A,B, hüpotenuus C, pindala S ja täisnurgast hüpotenuusile tõmmatud kõrguse H vahelisi seoseid võiks kirjeldada järgmise mudeliga:

kolmnurk(A,B,C,S,H):-
valem(A*A+B*B=C*C),
valem(S=(A*B)/2),
valem(S=(C*H)/2).

Otsitavate muutujate arvutamise käivitab predikaat arvuta(Mudel,Otsitavad), mis käivitab arvutusi sooritava predikaadi comp(Mudel, Otsitavad). Predikaat comp vaatab läbi kõik mudeli võrrandid ja püüab nende abil arvutada mõne (uue) muutuja väärtuse; pärast järjekordset läbivaatust käivitab ta end uuesti (lõpprekursiive predikaat); ta peatub, kui
- nimistus Otsitavad loetletud suuruste hulgas ei ole enam muutujaid (kõigil on väärtus); muutujate nimistust veel väärtustamata muutujate alamnimistu leiab süsteemipredikaat varsof;
- comp viimase käivitamise ajal ei õnnestunud enam väärtustada ühtki uut muutujat (töö jätkamine on mõtetu, ilmselt on mudel puudulik, s.t. ei sisalda kõikki vajalikke seoseid); selle tingimuse kontrolliks kirjutab comp enne järjekordset mudeli võrrandite läbivaatust mällu lause stop; kui õnnestub arvutada mõne uue muutuja väärtus, eemaldatakse see; kui comp järjekordsel käivitamisel on mälus lause stop,siis comp peatub - viimasel läbivaatusel ei õnnestunud enam arvutada ühtki uut muutujat. Et töö lõppedes oleks näha, milliseid valemeid millises järjekorras rakendati (tee valemite poolt määratud graafis), lisab comp iga uue muutuja arvutamisel kasutatud valemi valemite nimistusse Valemid, mis on predikaadi arvutused(Valemid) argument.

arvuta(Mudel,Otsitavad):-
retractall(stop), %võtame maha oletusena pandud lõpetusmägi
retractall(arvutused(_)),assert(arvutused([])),
retractall(mudel(_)),assert(mudel(Mudel)),
comp(Mudel,Otsitavad).

comp(_,_):-
clause(stop,true),!, %lõpetusmärk alles - midagi ei õnnestnud enam arvutada
arvutused(A),write(A).
comp(_,Otsitavad):-
free_variables(Otsitavad,[]),
!,arvutused(A1),reverse(A1,A),write(A).

comp(Mudel,Otsitavad):-
assert(stop), % paneme (oletusena) lõpetusmärgi
call(Mudel),
comp(Mudel,Otsitavad).

valem(Valem):-
rel(Valem),!, %midagi õnnestus arvutada
retractall(stop), %võtame peatusmärgi maha
retract(arvutused(A)),assert(arvutused([Valem|A])).

valem(_).

Sageli on ülesannet lihtsam kirjeldada mitme mudeli abil. Predikaat arvutamudelid(Mudelid, Otsitavad) töötab analoogiliselt ülalkirjeldatud predikaadiga comp: see käivitab mudeleid niikaua, kuini järjekordse kõigi mudelite läbivaatamise ajal veel õnnestus arvutada mõni uus muutuja, kui ühtegi uut muutujat enam ei õnnestunud arvutada, ta peatub. Kontrolliks lisab arvutamudelid esmakordsel käivitamisel mällu lause stop1; kui mingi mudeli läbivaatuse järel mälus pole mudelite peatamismärgendit - lauset stop, siis õnnestus selle mudeli abil midagi arvutada ja kogu mudelite nimistu peatumismärgend stop1 võetakse maha. Kui kõigi mudelite läbivaatuse järel mälus enam pole lauset stop1, siis õnnestus viimase mudelite läbivaatuse ajal midagi arvutada ja kogu mudelite nimistu Kõik_Mudelid käivitatakse uuesti.

arvutamudelid(Mudelid,Otsitavad):-
retractall(stop1),
assert(stop1), %oletusena paneme peatumismärgendi
arvutamitu(Mudelid,Otsitavad,Mudelid).

arvutamitu([Mudel|Mudelid],Otsitavad,Kõik_Mudelid):-
arvuta(Mudel,Otsitavad),nl,
((clause(stop,true), %mudelis õnnesus midagi arvutada!
retractall(stop1)); %võtame peatuse maha
true),
arvutamitu(Mudelid,Otsitavad,Kõik_Mudelid).%järgmised mudelid

arvutamitu([],Otsitavad,Kõik_Mudelid):-
not(clause(stop1,true)),!, %mingi mudeli abil õnnestus midagi arvutada
assert(stop1), %paneme peatuse uuesti ja käivitame kõik mudelid veel kord
arvutamitu(Kõik_Mudelid,Otsitavad,Kõik_Mudelid).

arvutamitu(_,_,_). %viimasel mudelite läbivaatusel ei õnnestunud midagi enam arvutada

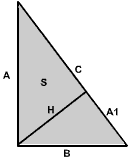Näiteks ülalesitatud täisnurkse kolmnurga kirjelduse abil kaateti A projektsiooni A1 leidmiseks peab seda mudelit kasutama kaks korda: - kogu kolmnurga ABC ja alamkolmnurga A1,H,A jaoks:

A=4,C=5,arvutamudelid([kolmnurk(A,B,C,S,H),kolmnurk(H,A1,B,S1,H1)],[A1]).
[6 = 5*2.4/2, 6 = 4*3/2, 4*4 + 3*3 = 5*5]
[3.84 = 4*1.92/2, 3.84 = 2.4*3.2/2, 2.4*2.4 + 3.2*3.2 = 4*4]

Kuna kasutatud valem lisatakse alati olemasolevate valemite ette (nimistu peaks), väljastatakse kõik valemite nimistud tagurpidi, s.t. eelmises näites on esimesena kasutatud valemit 4*4 + 3*3 = 5*5, siis 6 = 4*3/2 jne

Ülesandeid:

Punktides A,B,C on žarniirid; lõigud AB, BC on jäigad (nende pikkus ei muutu). Koosta mudel, mis võimaldaks arvutada punkti C x-koordinaadi punkti B kõrguse (y-koordinaadi) põhjal; testi näiteks andmetega AB=7, BC=5, OA=4, kasti K kõrgus (punkti C y-koordinaat) on 2 ja punkti B y-koordinaat - 5 (lahendamiseks võib kasutada kolmnurki AA1B, BC1C ja defineerida uue objekti, mis kirjeldab seoseid lõikude BA1,BC1,By,AA1,C1C,Cx,Cy vahel).

2.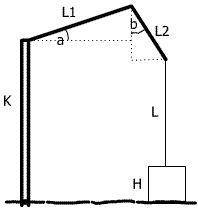Tee mudel kraana poolt tõstetava kasti põhja kõrguse (maast) leidmiseks, kui on teada kraana torni pikkus K, nokkade pikkused L1,L2, trossi pikkus L, nurgad a,b ja kasti kõrgus H; testi näiteks andmetega a=30, b=45 (kraadides), K=8, L1=4, L2=2, H=2 (meeldetuletuseks - täisnurkses kolmnurgas kaatet/hüpotenuus = vastasnurga siinus).

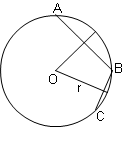Läbi iga kolme mitte ühel sirgel asetseva punkti saab (üheselt) panna rigjoone; selle keskpunkt on punkte paarikaupa ühendavate lõikude keskristsirgete lõikepunktis; punktide A(Ax,Ay), B(Bbx,By), C(Cx,Cy) koordinaadid määravad keskpunkti O(Ox,Oy) koordinaadid ja ringi raadiuse R ja ka vastupidi, kui on (näiteks) teada keskpunkti koordinaadid, ringi raadius ja Ax, siis saab leida Ay (siin võib tulla kaks võimalikku väärtust) või kui on teada punktide A ja B koordinaadid, keskpunkt ja Cx, siis saab leida raadiuse R ja koordinaadi Cy. Koosta arvutusmudel, mis kirjeldab kõik seosed suuruste Ax,Ay,Bx,By,Cx,Cy,Ox,Oy,R vahel ja võimaldab ükskõik milliste (piisava arvu) teadmisel arvutada ülejäänud suurused; testi näiteks ülalesitatud sõltuvuste abil (ilmutamata võrrandite lahendamiseeskirju peab täiendama ruutjuure arvutamisega!).

Küsimused, probleemid: