


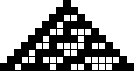 Ülemine rida on kahendarvudena järjestatud reegli eeldused (raku vasakpoolse naabri, raku enda ja tema parempoolse naabri olekud),
alumine (raku olek järgmisel hetkel)
annab reegli numbri. Kui automaadi tööd kujutada ridadena, kus iga järgnev rida on eelmise rea konfiguratsioonist
järgmisel sammul saadav konfiguratsioon, saame näiteks ühest elusrakust (olek 1) koosnevast konfiguratsioonist reegli 30 põhjal
arvutama hakates 10 sammuga kõrvaloleva kujundi (olek 1 - must ruut, 0 - valge).
Ülemine rida on kahendarvudena järjestatud reegli eeldused (raku vasakpoolse naabri, raku enda ja tema parempoolse naabri olekud),
alumine (raku olek järgmisel hetkel)
annab reegli numbri. Kui automaadi tööd kujutada ridadena, kus iga järgnev rida on eelmise rea konfiguratsioonist
järgmisel sammul saadav konfiguratsioon, saame näiteks ühest elusrakust (olek 1) koosnevast konfiguratsioonist reegli 30 põhjal
arvutama hakates 10 sammuga kõrvaloleva kujundi (olek 1 - must ruut, 0 - valge).
Wolframi põhitees on, et reeglite poolt määratud arenguprotsessi järgi jagunevad kõik
kõik (ühemõõtmeliste) rakuautomaatide reeglid nelja klassi:
- 1. klass: kõigi algkonfiguratsioonide korral areng stabiliseerub, kõik rakud kas
surevad välja või tekib mingi stabiilne muster;
- 2. klass: mitu võimalikku perioodiliselt korduvat lõppkonfiguratsiooni;
- 3. klass: areng näib ühtlaselt juhuslik, kuid selles korduvad alati lihtsad elemendid (kolmnurgad jne);
- 4. klass: korrapäraste ja juhuslike struktuuride segu; selle klassi automaadid realiseerivad universaalse arvuti:
kui kodeerida ükskõik milline programm (koos algandmetega) ja selle programmi väljund kahendjadadena, siis
leidub alati selle klassi rakuautomaat, mis teisendab (ühel sammul) sisendjada väljundisk, s.t. realiseerib
programmi.
Automaadi töö kirjeldamisel esitame rea (konfiguratsiooni mingil hetkel nimistuna). Eeldatakse, et kõik rakud, mis konfiguratsioonis ei esine, on olekus 0 - muidu ei oleks näiteks ühest rakust koosneva algkonfiguratsiooni korral määratud, milleks teisenevad selle raku parem- ja vasakpoolne naaber. Sellepärast lisame enne rea (konfiguratsiooni) teisendamist selle algusesse ja lõppu kaks 0-i; tänu sellele võib reegli rakendamist kirjeldada vaid kolmikutele ja lõpetada, kui teisendatava nimistu pikkus on väiksem kui 3:
kohanda(R,[0,0|R1]):-
append(R,[0,0],R1).
rakenda(L,L1,L1):-
length(L,P),P<3,!.
rakenda([X1,X2,X3|L],L1,LL):-
reegel([X1,X2,X3],Y),
append(L1,[Y],LY),
rakenda([X2,X3|L],LY,LL),!.
Predikaat arvuta_read(Algkonfiguratsioon, Read, N) arvutab algkonfiguratsioonist alates N rida ja salvestab need ridade nimistus Read; et ridade väljajoonistamine oleks lihtsam, salvestatakse koos iga uue reaga ka selle nihe (mitu ruudupikkust see rida on esimesega võrreldes vasakule nihkunud):
arvuta_read1(Ls,Ls,N,N):-!.
arvuta_read1([[L,Nihe]|Ls1],Ls,N1,N):-
uus_rida(L,L1),
Nihe1 is Nihe - 1, N2 is N1 +1,
arvuta_read1([[L1,Nihe1], [L,Nihe]|Ls1],Ls,N2,N).
Ridade ekraanile joonistamine algab uue akna loomisega; et hiljem (käsuga puhasta või clear) seda lihtne oleks leida, salvestatakse viit aknale predikaadis aken) :
joonista_read([],_,_,_,_):-!.
joonista_read([[L,Nihe]|Ls],N,Kylg,Keskp,P):-
joonista_rida(L,Nihe,N,Kylg,Keskp,P),
N1 is N - 1,
joonista_read(Ls,N1,Kylg,Keskp,P).
joonista_rida(L,Nihe,N,Kylg,Keskp,P):-
length(L,Pikkus),
X is Keskp - round(Kylg*Pikkus/2)+N,
Y is N*(Kylg-1) + 10, %algab 10 pikselit ylaäärest, ylemine-alumine katavad
joonista_rida1(L,X,Y,Kylg,P).
joonista_rida1([],_,_,_,_):-!.
joonista_rida1([R|L],X,Y,Kylg,P):-
colors(R,Color),
send(P, display, new(Nme, box(Kylg,Kylg)),point(X,Y)),
send(Nme,fill_pattern,Color),
X1 is X+Kylg-1, %1 pixel - ruutude küljed katavad üksteist
joonista_rida1(L,X1,Y,Kylg,P).
puhasta:-
aken(A),
send(A,clear).
clear :- puhasta.
test:-
reeglid(110,2),
joonista([1],100).
colors(0,colour(white)).
colors(1,colour(black)).
reeglid(N,B):-
retractall(reegel(_,_)),
reegli_list(N,B,L),
length(L,P1),
P is P1-1,
genereeri(L,B,P),
P2 is (B**3)-1,
(P<P2,!,genereeri1(P2,P,B));true.
% järgnevas luuakse reegli vasakute poolte nimistu
reegli_list(N,B,L):-
int_to_atom(N,B,Na),
int_to_atom(B,Ba),
atom_concat(Ba,'\'',Pref),
atom_concat(Pref,L1,Na),
atom_chars(L1,L).
genereeri([],_,_):-!.
genereeri([E|L],B,P):-
vasak(P,B,Arg),
atom_number(E,En),
assert(reegel(Arg,En)),
P1 is P-1,
genereeri(L,B,P1).
genereeri1(P,P,_):-!.
genereeri1(P2,P,B):-
vasak(P2,B,Arg),
assert(reegel(Arg,0)),
P1 is P2-1,
genereeri1(P1,P,B).
vasak(P,B,Arg):-
reegli_list(P,B,Arg1),
atoms_to_numbers(Arg1,Arg2),
pikenda(Arg2,Arg).
pikenda([E],[0,0,E]):-!. %lisa nulle, kui tulemus on liiga lühike
pikenda([E1,E2],[0,E1,E2]):-!.
pikenda(L,L).
atoms_to_numbers([],[]):-!. %teisenda aatomid täisarvudeks
atoms_to_numbers([A|L],[An|Ln]):-
atom_number(A,An),
atoms_to_numbers(L,Ln).
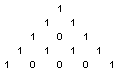 Leia reegel, mis realiseerib Pascali kolmnurga (kahendsüsteemis
esitatuna); Pascali kolmnurga esimene rida on [1] ja igas järgnevas saadakse numbrid kahe selle kohal
oleva numbri summeerimisel mod 2 järgi (tühi koht samastatakse 0-ga):
Leia reegel, mis realiseerib Pascali kolmnurga (kahendsüsteemis
esitatuna); Pascali kolmnurga esimene rida on [1] ja igas järgnevas saadakse numbrid kahe selle kohal
oleva numbri summeerimisel mod 2 järgi (tühi koht samastatakse 0-ga):
 ©2004
Jaak Henno
©2004
Jaak Henno