Abstraktse süntaksi puu

Grammatika teisendamisel analüüsiks sobivale (ükskõik, kas alt-üles või ülalt-alla) kujule tuleb tavaliselt juurde produktsioone ja mitteterminale, mis on vajalikud vaid analüüsi üheseks muutmiseks või kiirendamiseks. Selliste grammatikate alusel saadud derivatsioonipuudes on palju ülearuseid tippe. Näiteks grammatika

avaldis yksl avald_l
avald_l + yksl avald_l |
yksl tegur yksl_l
yksl_l * tegur yksl_l |
tegur (avaldis) | a

sobib hästi ülalt-alla analüüsiks (see on LL(1)), kuid selle abil saadud aritmeetilise avaldise a + a * (a) derivatsioonipuu sisaldab väga palju ülearuseid tippe:

Selle avaldise struktuur, oluline informatsioon on esitatav palju väiksema puuga: 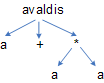- kõik ülejäänu on ülalesitatud puus ülearune.

Kuna kõik edasised tegevused põhinevad derivatsioonipuu läbimisel, aeglustaksid ülearused tipud transleerimise järgnevaid etappe - interpreteerimist või väljundkoodi genereerimist. Sellepärast toimub pärast süntaksianalüüsi puu moodustamist selle teisendamine nn abstraktse süntaksi puuks (AST - Abstract Syntax Tree). Abstraktse süntaksi puu kirjeldab vaid olulist informatsiooni, selle moodustamisel:

- visatakse välja kõik lineaarsed tipud, s.t. tipud, milles ei toimu hargnemisi;

- visatakse välja kõik tipud, mis ei genereeri väljundit (mis redutseeruvad tühjaks sõnaks

);

- visatakse välja kogu nn. süntaktiline suhkur (syntactic sugar), s.t. lähtekeele võtmesõnad, ebaolulised eraldajad (näiteks ülal sulud) jne;

- viiakse funtsionaalsümbolid (aritmeetilised operatsioonid, omistamine jne) vastava alampuu tippu, nii et nende argumendid jäävad alampuudeks.

Näiteks omistuslause (assignment) Ident := avaldis on tegelikult kahe argumendiga funktsioon ja selle abstraktne süntaks on

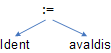
Tingimuslause if tingimus then käsud else käsud on kolme argumendiga funktsioon (kahe, kui else-osa puudub) ja selle abstraktne süntaks on

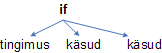
Vastavalt teisendatakse ka süntaksi kirjeldamiseks kasutatavat grammatikat. Kuna derivatsioonipuu on juba leitud, ei ole nüüd enam olulised analüüsiks kasutatud grammatikale esitatud nõuded - et ta oleks ühene ja võimaldaks kiiret analüüsi. Abstraktset süntaksit kirjeldatakse väga sageli mitmeste grammatikatega, näiteks aritmeetilise avaldise grammatika võib olla

Abstraktse süntaksi puu on väga sobiv lähteteksti või selle osade (näiteks aritmeetiliste avaldiste) teisendamiseks nn poola kujule, s.t. kujule, kus funktsionaalse avaldise kirjutamisel loetletakse algul argumendid ja viimasena funktsioon (lõppjärjestus tavalise binaarsete aritmeetiliste avaldiste kirjutamisel kasutatava keskjärjestuse asemel), näiteks

a + b oleks poola kujul ab+

a + 2*b oleks poola kujul a 2 b * +

sin(2*a) + cos(3*b) oleks poola kujul 2 a * sin 3 b * cos +

if a > b then x := y + z oleks poola kujul a b > x y z + := if

( := ja if on kahe argumendiga funktsioonid) jne.

Poola kuju on väga sageli kasutatav vahekuju, mida kasutatakse näiteks sisendprogrammi esitamiseks enne interpreteerimist. Poola kujul esitatud avaldise väärtuse arvutamine on lihtne realiseerida magasini abil: niipea, kui poola kujul esitatud avaldist vasakult paremale lugedes (s.t. avaldise sümboleid magasini surudes) on jõutud funktsionaalsümbolini, on selle all (ees) vastava funktsiooni argumendid ja nad kõik tuleb asendada vastava funktsiooni väärtusega; pärast seda võib protsessi jätkata.

Poola kuju saamiseks tuleb esitada avaldise abstraktse süntaksi (s.t. avaldise semantika) puu lõppjärjestuses (endorder); lõppjärjestuse algoritm on :
1. loetle vasakult paremale (lõppjärjestuses) alampuud;
2. loetle puu tipp.

Näiteks avaldise a + b * (c) abstraktse süntaksi puu tippude läbimisel lõppjärjestuses saame tippude järjekorraks
a b c * +

Eespool oli esitatud lihtsa programmeerimiskeele Pisi-Algoli (konkreetse) süntaksi grammatika; järgnevas on keelt veidi laiendatud, lubades if-lausel ka else-osa; avaldise struktuur on esitatud kujul, mis rahuldab LL(1)-tingimusi ja tagab aritmeetiliste operatsioonide +, -, *, / prioriteetide korrektse interpretatsiooni:

Programm Käsk;
Programm Käsk; Programm
Käsk Omistamine | Tingimuskäsk | Tsükkel | Kirjutamine | Lugemine
Omistamine Identifikaator := Avaldis
Identifikaator Täht | Indentifikaator (Täht | Number )
Avaldis Yksliige Avald_jatk
Avald_jatk λ | Add_op Avaldis
Yksliige Tegur Yksl_jatk
Tegur Identifikaator | Konstant | (Avaldis) | Aste
Yksl_jatk λ | Mult_op Yksliige
Aste (Tegur ^ Tegur )
Add_op + | -
Mult_op * | /
Number nool 0| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Täht nool A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Konstant Number | Number Konstant
Tingimuskäsk IF tingimus then_osa
then_osa THEN programm ENDIF | THEN programm ELSE programm ENDIF
Tingimus Avaldis Tingimusop Avaldis
Tsükkel FOR Omistamine UNTIL Avaldis DO Programm ENDLOOP
Tingimusop = | > | <
Kirjutamine WRITE Identifikaator
Lugemine READ Identifikaator

Selle (laiendatud) keele minimaalne abstraktse süntaksi grammatika võiks olla selline:

Semantiliste tegevuste kirjeldamisel jääb selline minimaalne kuju siiski sageli veidi liiga minimaalseks. Näiteks ühekäsulise programmi

if a > 0 then x := 1 else y := 2

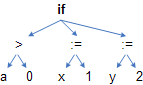if_AST 1 transleerimisel saame selle minimaalse abstrakste süntaksi kirjelduse põhjal kõrvaloleva puu. Kuid semantiliste tegevuste kirjeldamiseks jääb see puudulikuks; näiteks tingimuse a > 0 transleerimise järel peaks väljundisse genereerima kaks suunamislauset:

IF loogiline GOTO ...
GOTO ...

Siin loogiline on tingimuse arvutamise järel saadud loogiline väärtus, TRUE või FALSE ja esimene GOTO peaks juhtima esimese omistamise x := 1 transleerimise järel saadavate käskude algusesse, kuid teine GOTO - nende lõppu, s.t. omistamise y := 2 transleerimisel saadavate käskude algusesse.

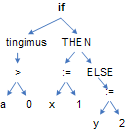if_AST 2 Kuid kui tingimuses oleks lubatud ka loogilised operaatorid (AND, IF, ...), siis puu läbimisel (lõppjärjestuses) pole võimalik teada, et võrratus > on kogu if-lause tingimusosa kõige ülemine tipp ja siin peab genereerima suunamiskäsud - võibolla on (kõrgemal) veel loogilised operaatorid. Samasugune olukord tekib esimese omistamise x := 1 transleerimise järel - siin peaks genereerima GOTO-käsu, mis juhib teisest omistamisest y := 2 üle, kuid taas pole teada, kas if-lause then-osas ei järgne veel mingeid käske. Ka ülalesitatud puu struktuur pole otstarbekas: x := 1 transleerimise järel omistamisest y := 2 üle suunava GOTO käsu genereerimisel oleks tarvis teada else-osa, s.t. y := 2 transleerimisele järgneva järgmise (vaba) rea numbrit; selle saaks (lihtsamini) siis, kui else-käsud on then-osa alampuu. Sellepärast ei kasutatata abstrakse süntaksi puu moodustamisel alati "kõige minimaalsemat" versiooni; kiire väljundkoodi genereerimiseks on näiteks eespoolesitatud puu asemel märksa mugavam kõrvalolev puu. Vastavalt peaks muutma ka abstrakse süntaksi kirjeldust; selliseid praktika jaoks "sobivalt" minimaalseid AST-puid on esitatud vastavate programmikonstruktsioonide Antlr-i abil transleerimise näidetes.

Koos abstrakste süntaksi puu moodustamisega toimuvad ka nn semantilised kontrollid. Paljud programmeerimiskeeltes korrektse programmi omadused ei ole (lihtsalt) kirjeldatavad kontekstivaba grammatikaga, s.t. neid ei saa kontrollida nimede tabeli moodustamise ja süntaksianalüüsi ajal. Sellised on näiteks nõuded suunamistele: GOTO käsule järgnev märgend peab esinema programmis täpselt ühes kohas (üks kord) ja GOTO ei või suunata alamprotseduuri sisse. Selliste tingimuste kontroll nõuab sageli eraldi mälustruktuuride kasutamist ja/või abstraktse süntaksi puu läbimist.

Ülesandeid:

1. Millised on AST puud pre-post suurendamis-vähendamisoperaatoritele ++x, x++, --x, x-- ?

Küsimused, probleemid: