Alt-üles analüüsi korral on kõige tähtsam
samm töödeldavas stringis aluse (mingi produktsiooni
parema poole) tunnistamine. Selleks on välja töötatud
palju algoritme; ühed kiirematest on eelnevusrelatsioonide 

 kasutamisel põhinevad algoritmid.
Eelnevusrelatsioone kasutavaid algoritme on mitmeid, vaatleme
järgnevas algoritmi, mis põhineb nn lihtsa
eelnevusgrammatika kasutamisel; seda algoritmi kasutati ka TTÜ-s
loodud translaatorite kompileerimise (compiler compiler) süsteemis
ELMA.
kasutamisel põhinevad algoritmid.
Eelnevusrelatsioone kasutavaid algoritme on mitmeid, vaatleme
järgnevas algoritmi, mis põhineb nn lihtsa
eelnevusgrammatika kasutamisel; seda algoritmi kasutati ka TTÜ-s
loodud translaatorite kompileerimise (compiler compiler) süsteemis
ELMA.
Relatsioon  on binaarne relatsioon
kõigi terminalide ja mitteterminalide hulgal: U
on binaarne relatsioon
kõigi terminalide ja mitteterminalide hulgal: U  V, kui
leiduvad produktsioonid
V, kui
leiduvad produktsioonid
 X
X  uUYv
uUYv
Y  Vw
Vw
See tähendab, et kui redutseeritavas sõnas on
järjest sümbilid ...UV...
ja U  V,
siis sümbolist V algab uus
alus. Suhte U
V,
siis sümbolist V algab uus
alus. Suhte U  V arvutamiseks tuleb
V arvutamiseks tuleb
a) leida produktsioonide paremates pooltes kõik
kõrvutiseisvate sümbolite paarid (U,Y), kus teine sümbol Y on mingi mitteterminal;
b) leida mitteterminali Y jaoks
kõik grammatika sümbolid V,
millega võib alata mingi Y-st
saadav string;
c) märkida suhe U  V kõigi selliste sümbolite
vahele.
V kõigi selliste sümbolite
vahele.
Relatsioon  on binaarne relatsioon
kõigi terminalide ja mitteterminalide hulgal: U
on binaarne relatsioon
kõigi terminalide ja mitteterminalide hulgal: U  V, kui
leidub produktsioon
V, kui
leidub produktsioon
X  uUYv
uUYv
See tähendab, et sümbolid U, V kuuluvad samasse alusesse (s.t. alus jätkub).
Relatsioon  on binaarne relatsioon, mille
teine liige on terminal; U
on binaarne relatsioon, mille
teine liige on terminal; U  a (a on terminal !) kui leiduvad
produktsioonid
a (a on terminal !) kui leiduvad
produktsioonid
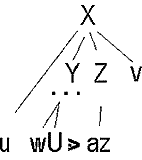 X
X  uYZv
uYZv
Y  wU
wU
Z  az
az
Z = a
See tähendab, et sümboliga U
lõpeb alus. Suhte U  a arvutamiseks tuleb:
a arvutamiseks tuleb:
a) leida produktsioonide paremates pooltes kõik
järjestikused sümbolite (Y,Z)
paarid, kus esimene sümbol Y
on mitteterminal
b) leida kõik sümbolid U,
mis võivad tekkida Y-st
saadud stringi lõppu (derivatsioonis tehakse vähemalt
üks samm!)
c) kui paari teine sümbol Z
on mitterminal, leitakse kõik terminalid a, mis võivad tekkida Z-st saadud stringi alguses (või
on Z ise terminal a)
d) märkida suhe U  a kõigi selliste paaride vahele.
a kõigi selliste paaride vahele.
Grammatikat nimetatakse eelnevusgrammatikaks, kui:
1) kõik eelnevusrelatsioonid on üheselt määratud,
s.t. mitte mingite sümbolite U,V
vahel ei või olla kaht erinevat eelnevusrelatsiooni
(võibolla ei ole ühtegi!);
2) grammatikas ei ole kaht sama parema poolega reeglit X  U, Y
U, Y  U;
U;
3) grammatikas ei ole tühja parema poolega reegleid X 
 v.a. juhul, kui X on algussümbol ja X ei esine ühegi reegli paremal
poolel.
v.a. juhul, kui X on algussümbol ja X ei esine ühegi reegli paremal
poolel.
Eelnevusgrammatika puhul on alt-üles analüüs lihtne: igal sammul loetakse analüüsitavat stringi vasakult paremale, kuni leitakse sümbolite jada
U  V1
V1  V2
V2  V2
...
V2
...  Vn
Vn  a
a
 V1V2V2
... Vn, seega asendatase string V1V2V2 ... Vn
mitteterminaliga X; selliselt
jätkates peab analüüsi lõppedes tekkima string #S#, kus S
on grammatika algussümbol (#
on sümbol, millega analüüsitav string piiratakse
mõlemalt poolt enne analüüsi algust).
V1V2V2
... Vn, seega asendatase string V1V2V2 ... Vn
mitteterminaliga X; selliselt
jätkates peab analüüsi lõppedes tekkima string #S#, kus S
on grammatika algussümbol (#
on sümbol, millega analüüsitav string piiratakse
mõlemalt poolt enne analüüsi algust).
Näide 1. Grammatika
X  aXXb | c
aXXb | c
|
X |
a |
b |
c |
# |
|
|
X |
 |
 |
 |
 |
|
|
a |
 |
 |
 |
||
|
b |
 |
 |
 |
 |
|
|
c |
 |
 |
 |
 |
|
|
# |
 |
 |
Sõna acaccbb alt-üles analüüsil tehakse järgmised sammud:
#acaccbb#  #
#  acaccbb#
acaccbb#
 #
#  a
a  caccbb#
caccbb#  #
#  a
a  c
c
 accbb#
accbb#  #
#  a
a  X
X
 accbb#
accbb#  ... #
... #  a
a  X
X
 a
a  c
c  cbb#
cbb#  ... #
... #  a
a  X
X
 a
a  X
X  c
c  bb#
bb#  ... #
... #  a
a  X
X
 a
a  X
X  X
X  b
b b#
b#  ... #
... #  a
a  X
X
 X
X  b
b #
#  #
#  X
X  #
#  OK
OK
Näide 2. Grammatika
T  a X | b Y | TT |
a X | b Y | TT | 
X 0 X | 1
0 X | 1
Y 0 Y | 1
0 Y | 1
T  T1 |
T1 | 
T1  a X | b Y | TT
a X | b Y | TT
X 0 X | 1
0 X | 1
Y 0 Y | 1
0 Y | 1
Avaldis  Term | Term +
Avaldis | Term - Avaldis
Term | Term +
Avaldis | Term - Avaldis
Term  Tegur | Tegur * Term | Tegur / Term
Tegur | Tegur * Term | Tegur / Term
Tegur  Ident | Const | (Avaldis)
Ident | Const | (Avaldis)
Avaldis  Term
Avaldise_lõpp
Term
Avaldise_lõpp
Term  Tegur Termi_lõpp
Tegur Termi_lõpp
Tegur  Ident | Const | (Avaldis)
Ident | Const | (Avaldis)
Avaldise_lõpp  + Avaldis | - Avaldis
|
+ Avaldis | - Avaldis
| 
Termi_lõpp  * Term | / Term |
* Term | / Term | 
Avaldis  Avaldis + Yksl
| Yksl
Avaldis + Yksl
| Yksl
Yksl  Yksl * Tegur | Tegur
Yksl * Tegur | Tegur
Tegur  Ident | Const | ( Avaldis )
Ident | Const | ( Avaldis )
Avaldis  Avaldis +
Yksl1 | Yksl1
Avaldis +
Yksl1 | Yksl1
Yksl1  Yksl
Yksl
Yksl  Yksl * Tegur | Tegur
Yksl * Tegur | Tegur
Tegur  Ident | Const | ( Avaldis )
Ident | Const | ( Avaldis )
S  0S11 | 011
0S11 | 011
S  if Tingimus then
S else S | S ; S |
if Tingimus then
S else S | S ; S | 
Tingimus  Boolean | Tingimus or
Boolean | Tingimus and Boolean
Boolean | Tingimus or
Boolean | Tingimus and Boolean
Boolean  0 | 1
0 | 1
number  0|1|2|3|4|5|6|7|8|9
0|1|2|3|4|5|6|7|8|9
numbrid  number | number numbrid
number | number numbrid
r_arv  numbrid | numbrid "." numbrid
numbrid | numbrid "." numbrid
number  0|1|2|3|4|5|6|7|8|9
0|1|2|3|4|5|6|7|8|9
numbrid  number | number numbrid
number | number numbrid
r_arv  numbrid kümnendosa
numbrid kümnendosa
kümnendosa  "." numbrid
"." numbrid
 ©2004 Jaak
Henno
id Milline neist on a) LL(1); b) ei ole LL(k) ühegi ka korral; c) on
eelnevusgrammatika ? Kui mõnda neist on lihtne väikese
modifikatsiooniga muuta LL(1)
või eelnevusgrammatikaks, esita see modifikatsioon!
©2004 Jaak
Henno
id Milline neist on a) LL(1); b) ei ole LL(k) ühegi ka korral; c) on
eelnevusgrammatika ? Kui mõnda neist on lihtne väikese
modifikatsiooniga muuta LL(1)
või eelnevusgrammatikaks, esita see modifikatsioon!
 ©2004 Jaak
Henno
©2004 Jaak
Henno