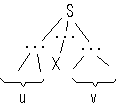Kiiret ülalt-alla analüüsi võimaldavad grammatikad

Ülalt-alla analüüsis ainuke situatsioon, kus midagi võib minna valesti (s.t. hiljem võib tekkida vajadus tagurdamiseks), on situatsioon, kus arendava mitteterminali (s.t. "pooliku" derivatsioonipuu esimese "rippuva" mitteterminali) jaoks on olemas mitu produktsiooni, kus see mitteterminal on vasakul, näiteks X  v | v'

Sellisel juhul on loomulik proovida mitteterminali arendamiseks kasutatav produktsioon valida analüüsitava terminalidest koosneva stringi k-tähelist algusosa kasutades.

Olgu x mingi terminalidest ja mitteterminalidest koosnev string; funktsiooni FIRSTk(x) väärtuseks on kõigi x-st tuletatavate terminalidest koosnevate stringide k-täheliste algusosade hulk. Kuna tavaliselt x on mingi produktsiooni X  x parem pool, kasutatakse FIRSTk(x) asemel sageli tähistust FIRSTk(X  x ), kuid selline tähistus määrab juba ka stringi x konteksti - x saadakse mitteterminali X asendamisel, s.t. selle kontekst on X kontekst; kuna x võib tekkida ka mõnel teisel viisil (mitte asendusest X x), võib hulk FIRSTk(X  x ) olla väiksem kui hulk FIRSTk(x).

Kui x-st saab ka sõnu, mille pikkus on < k (näiteks kui x   ), on tarvis FIRSTk(x) arvutamiseks teada ka X-i parempoolset konteksti (s.t. sümboleid, mis võivad X-le järgneda. k-tähelisi x-le järgnevate stringide hulka tähistatakse FOLLOW k(x) ja see kontekst lisatakse siis funktsiooni FIRST esimesele argumendile, aga teise argumendina näidatakse X arendamiseks kasutatav produktsioon (vt näide 2. allpool).

Kontekstivaba grammatikat nimetatakse LL(k) grammatikaks, kui iga kahe derivatsiooni

S  uXw  uvw
S  uXw  uv'w

korral sellest, et FIRSTk(vw) = FIRSTk(v'w) järeldub, et v = v', s.t. FIRSTk(vw) määrab X-i arendamiseks kasutatava produktsiooni üheselt.

Kõige sagedamini kasutatakse LL(1) grammatikaid, sest nende kasutamisel on analüüs kõige kiirem (tarvis on analüüsitavas stringis ette vaadata vaid üht sümbolit).

Kui grammatikas ei ole tühja parema poolega produktsioone (s.t. pole produktsioone kujul X  ), võib LL(1) tingimuse esitada palju lihtsamal kujul: grammatika on LL(1), kui kõigi sama vasema poolega produktsioonide

X  w1 | w2 | ... | wn

jaoks FIRST1(wj)  FIRST1(wi) = 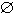  ( i  j ).

Grammatikat nimetatakse lihtsaks LL(1) grammatikaks, kui selles ei ole tühja parema poolega reegleid X  ja kõigi sama vasaku poolega reeglite X  w1 | w2 | ... | wn korral see tingimus on täidetud, s.t. kõik alternatiivid w1, w2, ... , wn algavad erinevate terminalidega.

Näide 1. Grammatika

S  aXS | b
X  a | bSX

on lihtne LL(1) grammatika.

Näide 2. Vaatleme grammatikat

S  | abA
A  Saa | b

Kuna mitteterminalist S võib saada tühja sõna , on FIRSTk(S) leidmiseks tarvis analüüsida mitterminali S kõiki parempoolseid kontekste, s.t. stringe, mis võivad tekkida S järel (hulk FOLLOWk(S) ); kuna see hulk sõltub sellest, mis tuleb S järel (S-i parempoolsest kontekstist), uurime eraldi iga juhtu, kus S tekib (s.t. kõiki reeglite paremaid pooli, kus S esineb) ja lisame funktsiooni FIRST teiseks argumendiks mitteterminali arendamiseks kasutatud reegli parema poole:

FIRST1(Sa, ) = {a}, FIRST1(Sa, abA) = {a}

Kuna saime samad hulgad, ei ole see grammatika LL(1) grammatika, sest ühe sümboli ette vaatamisega ei ole võimalik otsustada, kas mitteterminal S kontekstis Sa tuleb arendada tühjaks sõnaks  või stringiks abA .

Vaatleme kaheelemendilisi alglõike:

FIRST2(Saa, ) = {aa}, FIRST1(Saa, abA) = {ab}

Kuna kaheelemendilised alglõigud on erinevad, on see LL(2) grammatika - kahe sümboli ette vaatamisega saab alati otsustada, milleks S tuleb arendada.

Näide 3. Uurime grammatikat

S  A | B
A aAb | 0
B  aBbb | 1

Lihtne on näha, et L(S) = {an0bn }  {an1b2n }, n=0,1,2,...

See tähendab, et see grammatika ei ole LL(k) -grammatika ühegi k korral, sest lõpliku (fikseeritud) pikkusega stringi vaatamisega ei ole võimalik otsustada, kas esimesel sammul kasutada produktsiooni S  A või S  B; seda saab teha alles siis, kui a-de jada järel loetakse 0 või 1, kuid a-de jada võib olla kuitahes pikk, s.t. see (esimesel sammul produktsiooni valikut määrav kontekst) võin olla kuitahes kaugel.

Näide 4 . Grammatika

S  aS | aB
B bB | b

genereerib keele

L(S) = {anbm, n,m N },

ja ka see grammatika ei ole LL(1) (see on LL(2)). Kuid (ühe produktsiooni muutmisega!) saab lihtsa LL(1) grammatika, mis genereerib sama keele:

S  aS | abB
B bB | b

s.t. grammatikat on võimalik (genereeritavat keelt muutmata) teisendada kujule LL(1), mis võimaldab kiiret ülalt-alla analüüsi.
Seda näidet on lihtne üldistada suvalise k jaoks, s.t. esitada grammatika, mis ei ole LL(k), kuid on teisendusega muudetav ekvivalentseks LL(1) - grammatikaks.

Näide 5 . Grammatika

S  aS | SB
B bB | b

genereerib keele

L(S) = {anbm, n,m N },

ja ka see grammatika ei ole LL(1) (see ei ole LL(k) ühegi k korral). Kuid (ühe produktsiooni muutmisega!) saab lihtsa LL(1) grammatika, mis genereerib sama keele:

S  aS | abB
B bB | b

s.t. grammatikat on võimalik (genereeritavat keelt muutmata) teisendada kujule LL(1), mis võimaldab kiiret ülalt-alla analüüsi.
Seda näidet on lihtne üldistada suvalise k jaoks, s.t. esitada grammatika, mis ei ole LL(k), kuid on teisendusega muudetav ekvivalentseks LL(1) - grammatikaks.

On lihtne näha, et LL(k) grammatika puhul saab ülalt-alla analüüsi teha lineaarse kiirusega (analüüsitava stringi pikkuse suhtes).

Ülesandeid:
1. Näidata, et grammatika

S  aAaa | bAba
A b | 

ei ole LL(1) ega LL(2), kuid on LL(3)-grammatika.
2. Näidata, et grammatika

S  aAaB | bAaB
A a | ab
B bB | bb

ei ole LL(1) ega LL(2), kuid on LL(3)-grammatika.
3. Näidata, et grammatika

S  Sa | b

ei ole LL(k) grammatika ühegi k korral (milliseid jadasid see grammatika genereerib?) ja teisendada see grammatika LL(1) grammatikaks.
4. Näidata, et grammatika

S  bA
A  aA | 

on eelmise ülesande grammatikaga ekvivalentne (genereerib sama keele) LL(1)-grammatika.
5. Grammatika on määratud produktioonidega

S A B C
A A a | b B
B B b |
C C c |

Millised järgnevatest väidetest on tõesed:

1) a FIRST1(S); 2) c FIRST1(Aa); 3) c FOLLOW1( A); 4) - see on kas LL(1) või LL(2) grammatika.

6. Näidata, et grammatika

S  aS | a

ei ole LL(1), kuid on LL(2)-grammatika. Koostada ekvivalentne (genereerib sama keele) LL(1) grammatika.
7. Kas grammatika


S  aA
A  S | 

on eelmise ülesande grammatikaga ekvivalentne LL(1)-grammatika?
8. Näidata, et grammatika

S  aaSbb | a |

on LL(2) grammatika ja leida sellega ekvivalentne LL(1) grammatika.
9. Kas vasakrekursiivne grammatika (s.t. reegliga X X... ) võib olla LL(k) grammatika (ükskõik millise k korral, v.t. ülesanne 3) ?
10. Kas järgnev grammatika on LL(2) või LL(3) grammatika (või pole kumbki)?

A aBC
B c | cd
C df | eg

11. Näidata, et keel

L = {anb2n }  {a2nbn }, n=0,1,2,...

ei ole genereeritav LL(k) grammatikaga (ühegi k korral, vt. näide 3).
12. Numbrilised suurused on:
- täisarvud (märgiga või ilma);
- reaalarvud; lubatud kujud oleks (näiteks) 3.14, -2., 0.1E-10, 2.1E2; lubatud ei ole kujud, kus puudub '.' või E järel (kui see on) pole numbreid, s.t. vigased on näiteks 2E+2, 3.1E;
- kompleksarvud kujul reaalosaiimaginaarosa, kus i on terminal ja reaalosa, imaginaarosa võivad olla täis- või reaalarvud;
- vahemikud kujul alaraja..ylaraja, kus alaraja ja ylaraja on kas täis- või reaalarvud ja .. on terminal .

Koosta LL(1) või LL(2) grammatika numbrilise suuruse kirjeldamiseks.

13. Programmeerimskeele Modula-2 käsu süntaks on kirjeldatud grammatikaga:

Statement CompoundStatement | Assignment | ProcedureCall
| IfStatement | WhileStatement
| WriteStatement | ReadStatement ProcedureCall ProcIdentifier
ProcIdentifier Identifier
Assighnment Identifier := Expression

(siin defineerimata mitteterminalid võib lugeda terminalideks).

See grammatika ei ole LL(1) - miks? Kas see grammatika on LL(2) ? Teisenda grammatika LL(1) -grammatikaks!

14. Programmeerimiskeele deklaratsioonide osa on kirjeldatud järgmise grammatikaga:

Program nool Declarations Function_declarations
Declarations nool Declaration Feclarations
| Declaration nool Type Identifier-list;
Identifier_list nool Identifier
| Identifier-list , Indentifier Identifier nool ident
| * Identifier Type nool int
| float
| char
| void Function_declarations nool Function_declaration Function_declarations
| Function_declaration nool Function_head Function_body
Function_head nool Type Identifier Arguments
Arguments nool ( Parameter_list )
| ( ) Parameter_list nool Parameter Parameter_list
| Parameter nool Type Identifier

Siin kirjeldamata mitteterminalid (ident, function_body) võib lugeda terminalideks; terminalid on ka kõik kirjelduses esinevad sulud ( ) .

See grammatika ei ole LL(1) - miks? Milline on minimaalne k, mille jaoks see grammatika oleks LL(k) grammatika?

Küsimused, probleemid: ©2004-2013 Jaak Henno