Lõplike keelte (keel on märgijadade hulk !) esitamiseks võib lihtsalt loetleda kõik keelde kuuluvad sõnad. Lõpmatute keelte esitamiseks tuleb kasutada mingit rekursiivset genereerimismehhanismi, mis
Kui me tahame loomulikus keeles defineerida mõistet (struktuuri) "lause", kasutame me abimõisteid "alus", "öeldis", "sihitis" jne. Ka eelmises peatükis vaadeldud loomuliku- ja programmeerimiskeele kirjeldused kasutasid selliseid abimõisteid; neid nimetatakse mitteterminalideks.
Näide 1. Oletame, et me tahame kirjeldada tähestikus T = {0,1} mõistet Paaris_kahendarv, s.t. sümbolitest 0,1 koostatud jadasid, mille lõpus on 0. Loomulik on algul defineerida abimõiste Kahendarv, mis on suvaline sümbolitest 0,1 koostatud jada:
Kahendarv  0 (s.t. kahendarv on sümbol 0)
0 (s.t. kahendarv on sümbol 0)
Kahendarv  1 (s.t.
kahendarv on sümbol 1)
1 (s.t.
kahendarv on sümbol 1)
Kahendarv  Kahendarv 0 (s.t. juba genereeritud kahendarvule kirjutatakse
lõppu 0 )
Kahendarv 0 (s.t. juba genereeritud kahendarvule kirjutatakse
lõppu 0 )
Kahendarv  Kahendarv 1 (s.t. juba genereeritud kahendarvule kirjutatakse
lõppu 1 )
Kahendarv 1 (s.t. juba genereeritud kahendarvule kirjutatakse
lõppu 1 )
Paaris kahendarv on Kahendarv, mille lõpus on 0:
Paaris_kahendarv  Kahendarv 0
Kahendarv 0
Eespoolesitatud definitsiooniridu Kahendarv
 0, Kahendarv
0, Kahendarv  1
jne nimetatakse produktsioonideks. Esituse
kompaktsemaks muutmiseks esitatakse sama vasaku poolega, s.t. sama
mitteterminali defineerivad produktsioonid tavaliselt nii:
1
jne nimetatakse produktsioonideks. Esituse
kompaktsemaks muutmiseks esitatakse sama vasaku poolega, s.t. sama
mitteterminali defineerivad produktsioonid tavaliselt nii:
Kahendarv  0 | 1 |
Kahendarv 0| Kahendarv 1
0 | 1 |
Kahendarv 0| Kahendarv 1
Näide 2. Täisarv (tähistame lühemalt: Int) on sümbolitest 0,1,2,3,4,5,6,7,8,9 koostatud jada, s.t. see on kas üks number või (lühem) täisarv, mille lõppu on kirjutatud veel üks number, seega täisarvu defineerimisel on otstarbekas kasutada abimõistet Number:
Number  0|1|2|3|4|5|6|7|8|9
0|1|2|3|4|5|6|7|8|9
Int  Number | Int Number
Number | Int Number
Reaalarv (Real) koosneb kahest täisarvust (reaalarvu täis- ja murdosa), mille vahel on murdosa eraldaja (programmeerimiskeeltes tavaliselt '.'):
Real  Int . Int
Int . Int
Produktsioonisüsteemid esinevad mitte ainult arvuti- ja keeleteaduses, nende abil on väga loomulik kirjeldada paljusid elus- ja eluta looduses toimuvaid protsesse ja nähtusi. Näiteks rakkude paljunemine (kasv organismis) sarnaneb produktsiooniga: rakk pooldub ja selle asemele tekib kaks (või enam) rakku. Hollandi bioloog Aristid Lindenmayer arendas eluslooduse vormide kirjeldamiseks formaalse süsteemi, mis põhineb produkstioonide kasutamisel.

 Taimede
arengut võib kirjeldada produktsioonidega, milles kasutatakse
mitteterminale
Taimede
arengut võib kirjeldada produktsioonidega, milles kasutatakse
mitteterminale
haar(n) -
arengutasemel n oleva oksahaara
kasvatamine (kui n=0, siis mitte
midagi) ja
vars(n) -
sirge oks, mille pikkus kahaneb n
kahanedes - vähem arengutsükleid läbinud (noorem) oks on lühem.
haar(n)  vars(n) [+
haar(n-1)] vars(n-1) [- haar(n-1)] [+ haar(n-1)]
vars(n) [+
haar(n-1)] vars(n-1) [- haar(n-1)] [+ haar(n-1)]
Produktsioon
haar(n)  vars(n) [- haar(n-1)] [+ haar(n-1)]
vars(n) [- haar(n-1)] [+ haar(n-1)]
Produktsioonide abil on lihtne kirjeldada ka paljusid looduses esinevaid fraktaalseid kõveraid ja pindu, s.t. kõveraid ja pindu, mille alamlõigud/osad sarnanevad kogu kõveraga - kui palju me ka ka ei suurendaks, suurenduses näeme (peaaegu täpselt) samasugust pilti; sellised jooned on näiteks rannajoon ja silmapiir.
 Näiteks
silmapiirijoone tekkimist võib kirjeldada produktsiooniga
Näiteks
silmapiirijoone tekkimist võib kirjeldada produktsiooniga
silmapiir(n)  silmapiir(n-1) silmapiir(n-1)
silmapiir(n-1) silmapiir(n-1)
Samasugust põhimõtet kasutavad digitaalseid maastikke genereerivad programmid (Bruce3D): alatakse tasapinnalise nelinurgaga; arengusamm (produktsioon) seisneb nelinurga keskpunkti nihutamist (kolmemõõtmelises ruumis) juhuslike paranduste dx, dy, dz võrra ja seejärel rakendatakse nelinurga igale veerandile sama algoritmi.
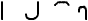 Käekirja
kirjeldamiseks ja analüüsiks on edukalt produktsioonisüsteemi, mis
kombineerib nelja joonekese kombineerimisel, s.t. neist "sõnade"
moodustamisel. Joonekesed on graafilise tähestiku "tähed", kuid
erinevalt tavalisest (trükitud) teskti moodustatamisest võib neid
"sõnas" sobiva nurga võrra keerata ja suurendada/vähendada - nii nagu
teevad ka inimesed käsitsi kirjutades.
Käekirja
kirjeldamiseks ja analüüsiks on edukalt produktsioonisüsteemi, mis
kombineerib nelja joonekese kombineerimisel, s.t. neist "sõnade"
moodustamisel. Joonekesed on graafilise tähestiku "tähed", kuid
erinevalt tavalisest (trükitud) teskti moodustatamisest võib neid
"sõnas" sobiva nurga võrra keerata ja suurendada/vähendada - nii nagu
teevad ka inimesed käsitsi kirjutades.
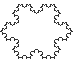 Geomeetriliste
kujundite korral on sageli arusaadavam kujutada kogu produkstioon
graafiliselt. Kui produktsioon on (näiteks) selline:
Geomeetriliste
kujundite korral on sageli arusaadavam kujutada kogu produkstioon
graafiliselt. Kui produktsioon on (näiteks) selline:


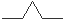
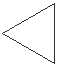 (produktsioone
sirglõikudele rakendades kohandatakse vasaku ja parema poole pikkused
asendatava lõigu pikkusega), saame paari derivatsioonisammu järel
lumehelbekese.
(produktsioone
sirglõikudele rakendades kohandatakse vasaku ja parema poole pikkused
asendatava lõigu pikkusega), saame paari derivatsioonisammu järel
lumehelbekese.
 {0,1}*,
w = 1w', |w|0 = |w|1 }.
{0,1}*,
w = 1w', |w|0 = |w|1 }.

 Milliste reeglite
järgi kasvavad kõrvalolevad puud?
Milliste reeglite
järgi kasvavad kõrvalolevad puud? R  I K
I K
I  0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 I | 1 I | 2 I | 3 I | 4 I | 5 I | 6 I | 7 I | 8 I | 9 I
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 I | 1 I | 2 I | 3 I | 4 I | 5 I | 6 I | 7 I | 8 I | 9 I
K  , I
, I
R  R 0 | R 1 | R 2 | R 3 | R 4 | R 5 | R 6 | R 7 | R 8 | R 9 | I , 0 | I , 1 | I , 2 | I , 3 | I , 4 | I , 5 | I , 6 | I , 7 | I , 8 | I , 9
R 0 | R 1 | R 2 | R 3 | R 4 | R 5 | R 6 | R 7 | R 8 | R 9 | I , 0 | I , 1 | I , 2 | I , 3 | I , 4 | I , 5 | I , 6 | I , 7 | I , 8 | I , 9
I  0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 I | I 1 | I 2 | I 3 | I 4 | I 5 | I 6 | I 7 | I 8 | I 9
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 I | I 1 | I 2 | I 3 | I 4 | I 5 | I 6 | I 7 | I 8 | I 9
 ©2004
Jaak Henno
©2004
Jaak Henno