Regulaarsed keeled

JFLAP - abivahend lõplike automaatide, reg. grammatikate ja avaldiste uurimisel

Programmeerimiskeelte leksika kirjeldatakse tavaliselt regulaarsete keelte abil. Need on keeled, mida saab kirjeldada (genereerida) regulaarse e. klass-3 grammatikaga (Chomsky klassifikatsioonis), s.t. grammatikaga (T,V,X₀,P), mille köik produktsioonid on kujul

Lekseemide (tokens) kirjeldamisel ja nende tunnistajate koostamisel kasutatakse ka teisi formalisme: regulaarseid avaldisi ja lõplikke automaate. Tunnistaja (recognizer) on programm, mis leiab programmi tekstis lekseemid. Regulaarsed avaldised ja lõplikud automaadid on samaväärsed regulaarsete grammatikatega - kui mingit keelt saab kirjeldada ühega nendest formalismidest, siis saab seda kirjeldada ka teistega. Erinevus on nende kasutamises: regulaarsed grammatikad ja regulaarsed avaldised on genereerimismehhanismid, s.t. nad kirjeldavad lekseemide struktuuri; automaat võimaldab kontrollida, kas sellele esitatud märgijada (automaadi sisend) on korrektselt kirjutatud lekseem.

Regulaarsed avaldised ja igale regulaarsele avaldisele e vastav keel L(e), s.t. sõnade hulk terminalide tähestikus T defineeritakse sammude kaupa rekursiivselt:

- tühi sõna λ on regulaarne avaldis, L(λ) = Ø (s.t. tühjale sõnale vastab tühi keel);
- iga x

T on regulaarne avaldis, L(x) = {x} (s.t. vastav keel koosneb ühest ühetähelisest sõnast);
- kui e₁, e₂,..., e_n on regulaarsed avaldised ja neile vastavad keeled L(e₁),L(e₂),...,L(e_n), siis ka:

1. (e₁ | e₂ | ... | e_n ) on regulaarne avaldis ja L((e₁| e₂ | ... | e_n )) =

L(e_i);
2. e₁e₂...e_n on regulaarne avaldis ja L(e₁e₂...e_n) = L(e₁)L(e₂)...L(e_n) (kõikvõimalikud n teguri korrutised, kus i-s tegur on keelest L(e_i), i=1...n );
3. e_i* on regulaarne avaldis (iga i = 1,2,...,n korral) ja L(e_i*) =

L(e_i^j), j = 0,1,2,...,
s.t. L(e_i*) = λ

L(e)

L(e²)

...

Regulaarsed grammatikad ja regulaarsed avaldised on formalismid keelte defineerimiseks ja keelde kuuluvate sõnade genereerimiseks (moodustamiseks). See on tavaliselt inimese jaoks väga arusaadav ja mõistetav viis, kuid genereerimismehhanismi olemasolu ei taga veel, et suvalise söna w ja (grammatika abil esitatud) keele L jaoks oleks alati selge, kuidas lahendada probleemi: kas sõna w kuulub keelde L, s.t. w

? L

Söna keelde kuuluvuse probleemi (aga seda peab arvuti lahendama igas keele teisendusprogrammis, s.t. kõigil transleerimise etappidel) kasutatakse automaate.

Igale grammatikate klassile Chomsky klassifikatsioonis vastab oma automaatide klass.

Regulaarseid keeli saab defineerida ka kui keeli, mida saab tunnistada lõpliku automaadiga. Löplik automaat on viisik (A, S, s₀, F, P), kus

A on sisendtähestik (terminalide tähestik);
S on (lõplik) olekute hulk ;
s₀

S on algolek;
F

S on lõppolekute hulk;
P on automaadi üleminekuid (tööd) kirjeldavate produktsioonide hulk. Produktsiooni sa

s' semantika (tähendus) on, et kui automaat olekus s loeb sisendlindilt sümboli (sisendtähestiku tähe) a, läheb ta olekusse s' .

Löplikke automaate esitatakse sageli nende graafiga. Automaadi graafi tippudeks on olekud, kaarteks - üleminekud, kaart tähistatakse sisendsümboliga, mis vastava ülemineku esile kutsub.

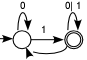
Näide 1. Täisarvud on sõnad tähestikus T = {0,1,2,3,4,5,6,7,8,9}. Neid kirjeldab:

- regulaarne avaldis(0|1|2|3|4|5|6|7|8|9)*
- lõplik automaat, mille graaf on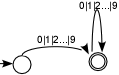

(automaadi graafis

tähistab algolekut,

- lõppolekut);

- regulaarse grammatikaga, mille ainus mitteterminal on Arv ja produktsioonid on
Arv

Arv 0|Arv 1|Arv 2|Arv 3|Arv 4|Arv 5|Arv 6|Arv 7|Arv 8|Arv 9|1|2|3|4|5|6|7|8|9
(Arv

Arv 1|Arv 2 ... on lühend produktsioonide Arv

Arv 1 , Arv

Arv 2 , ... kokkuvõtlikumaks esitamiseks).

Näide 2. Kui täisarvud ei või alata nulli(de)ga, siis selliseid täisarve kirjeldab

- regulaarne avaldis (1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*
- lõplik automaat, mille graaf on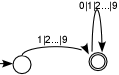

(koosta ise grammatika!).

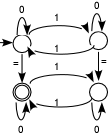Näide 3. Grammatika ({0,1,=}, {X₀ , Y, Y₁ }, X₀,
{X₀

Y = Y, Y

| Y 0 | Y₁ 1, Y₁

Y₁ 0 | Y 1} )
genereerib keele { w₁ = w₂ | |w₁|₁ = |w₂|₁(mod 2)}, s.t. kõikvõimalikud jadad kujul w₁ = w₂ , kus sõnades w₁ , w₂ on terminali 1 esinemiste arv sama paarsusega (|w|₁ tähistab terminali 1 esinemiste arvu sõnas w), s.t. kas mõlemates paaris või mõlemates paaritu arv. Selle keele tunnistab kõrvalolev automaat.

Mingit keelt kirjeldavad automaadid, grammatikad ja regulaarsed avaldised ei ole üheselt määratud ja sageli on (mingis mõttes) minimaalse regulaarse avaldise leidmine keelele üsna raske ülesanne. Näiteks regulaarse avaldisega (0*1+)*0* kirjeldatud keele tunnistab kõrvalolev automaat; regulaarse avaldise teise (vasakult paremale lugedes) iteratsiooni tähistamiseks on automaadis nn "tühi" üleminek (ilma sisendita). Kuid automaati uurides saab selgeks, et selle ülemineku võib eemalda, automaadi poolt tunnistatav keel sellega ei muutu. Kuid ilma selle tühja üleminekuta võib automaadi poolt tunnistatud keele esitada lihtsamalt: 0*1(0|1)*, seega. (0*1+)*0* = 0*1(0|1)*.

1. Ülaltoodud grammatika genereerib regulaarse keele (sest selle keele tunnistab esitatud lõplik automaat), kuid ei ole ise regulaarne, sest produktsioon X₀

Y = Y ei ole regulaarse grammatika produktsioon. Teisenda grammatikat, nii et muutuks regulaarseks.

2. Koosta regulaarne grammatika, regulaarne avaldis ja lõplik automaat kõigi binaarsüsteemis (tähestikus 0,1) esitatud neljaga jaguvate täisarvude genereerimiseks ja tunnistamiseks.

3. Paljudes programmeerimiskeeltes määratakse mõiste string järgmiste tingimustega:

- string on jutumärkide "..." vahele võetud tähtede, numbrite ja keeles lubatud märkide jada, milles ei esine (otse) jutumärgid, kuid võivad esineda interpreteeritavad (nn escape) märgid: \n (reavahetus), \t (tabulatsioon), \" (tähistab stringi teksti kuuluvaid jutumärke), \\ (tähistab stringi teksti kuuluvat märki \ ).

Koosta regulaarne avaldis stringide kirjeldamiseks ja lõplik automaat nende tunnistamiseks.

Lülitusskeemis kaks lülitit juhivad sama pirni - vajutus ükskõik kumma lüliti üleval olevale otsale muudab pirni oleku (põleb, ei) vastupidiseks (tavaline valgustuskeem näiteks trepil oleva valgust juhtimiseks nii trepi all- kui ka ülaotsast). Sisendsignaalideks (terminalideks) on v₁, p₁, v₂, p₂ (vajutused esimese või teise lüliti vasak- või parempoolsele otsale); algolekus on mõlema lüliti parempoolne ots üleval ja pirn ei põle. Keel koosneb kõikvõimalöikest terminalide v₁, p₁, v₂, p₂ jadadest, mis panevad pirni põlema (vajutused vöivad olla suvalises järjekorras lüliti olekust sõltumata), näiteks p₁, p₂, p₁ p₁ (viimane vajutus lambi olukorda ei muuda!), p₁p₂p₁v₂, p₁v₁v₁p₂, v₁v₂p₂ jne. Leia regulaarne grammatika ja lõplik automaat selle keele genereerimiseks ja tunnistamiseks.

5. Telefoninumber on 6-10 kohaline numbrite jada, milles esimesed kaks või kolm numbrit võivad olla sulgudes (maatunnus) ja nende järel, samuti enne kolme viimast numbrit võib olla üks tühik, seega korrektse vormiga (süntaksiga) telefoninumbrid on näiteks 3726203 402, (327) 642 387, (10)617851, kuid mitte 327-654892, 372 36 2594. Koosta regulaarne avaldis korrektselt kirjutatud telefoninumbrite kirjeldamiseks.

6. Kas grammatikaga

T a X | b Y | TT |
X 0 X | 0
Y 0 Y | 1

määratud keel on regulaarne?

Kui on, siis koosta lõplik automaat ja regulaarne avaldis selle kirjeldamiseks.

7. HTML-dokumendi päise süntaks on <head> päis </head> ja päis on määratud järgmiste tingimustega: selles peab olema täpselt üks tiitlielement (<title>string</title>), kõige rohkem üks baasi määrav element (<base string />) ja ükskõik kuimitu (null või rohkem) meta- (<meta string />), skripti- (<script>string </script>), stiilielementi (<style> string </style>) ja linki (<link string />); kõik need elemendid võivad esineda ükskõik millises järjekorras. Koosta regulaarne grammatika HTML-dokumendi päise kirjeldamiseks.

8. Assembler-i HLA üks trükikäskudest on stdout.put(argumendid), kus mitteterminal argumendid tähistab komadega üksteisest eraldatud nimistut stringidest (stringieraldajad on jutumärgid " "), reavahetussümbolitest nl, muutujatest (identifikaatoritest), registritähistustest eax, ebx, ecx, edx; muutuja ja registritähistuse järel võib olla kooloni : järel veel minimaalne väljatrükis kasutatava välja laius (täisarv 1..12); stdout.put lõpus võib olla määratud ka väljatrükitava identifikaatori või registrinime suurus baitides, kas i8, i16 või i32, seega väljatrükikäsu näited oleks

stdout.put( "Hello World", nl );
stdout.puti32(eax, ebx);
stdout.put( I, "-s Fibonacci arv on ", F2:6, nl );

Koosta regulaarne avaldis HLA väljatrükikäskude kirjeldamiseks.

9. Sageli püütakse informatsiooni kodeerida nii, et koodeering võimaldaks ka kontrollida - kas edastamise käigus mingeid vigu pole tekkinud? Kõige lihtsam selline kontroll on nn paarsuse kontroll - teatud arvu bittide järel (näit iga baidi lõpus) kontrollitakse, kas eelnenud viimases kontrollitavas lõigus oli paarisarv või paaritu arv bitte ja vastavalt sellel pannakse kontrollitava lõigu viimaseks bitiks kas 0 või 1.
Koosta regulaarne grammatika, lõplik automaat ja regulaarne avaldis keelele, mis koosneb bitijadadest, mille pikkus jagub neljaga ja kus iga neljas bitt kontrollib eelnenud kolme biti paarsust, s.t. kui eelnenud 3 bitti sisaldasid paarisarvu 1-sid, on neljas bitt 0, kui aga paaritu arvu, on neljas bitt 1.

Regulaarsed keeled, regulaarsed avaldised ja lõplikud automaadid