Arvutil ei ole mingit "oma arusaamist ", arvuti saab kõigest aru vaid talle esitatud märgi/bitijada struktuuri uurides. Ka programmilõikude semantika (tähenduse) saab leida ainult selle programmilõigu struktuuri abil. See struktuur kirjeldatakse grammatikaga ja programmilõigu tähenduset esitab selle programmilõigu süntaksi puu, s.t. derivatsioonipuu, mille põhjal see programmilõik saadakse grammatika algussümbolist.
Erinevad derivatsioonipuud annavad erineva tähenduse, näiteks aritmeetilisele avaldisele 1 + 2 * 3 saadakse erinevate puudega erinevad väärtused:
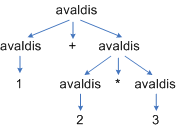

Esimese puu põhjal on kogu avaldise väärtus 7, aga teise puu põhjal 9. Loomulikult on selline erinevate interpretatsioonide võimalikkus lubamatu, kõik translaatorid peavad kõigis arvutites andma sama tulemuse.
Kõige olulisem nõue, mida süntaksit kirjeldavad grammatikad peavad rahuldama (sõltumata analüüsi meetodist) on grammatika ühesus (non-ambiquity) - igal grammatika abil genereeritud programmil (programmilõigul) võib olla vaid üks derivatsioonipuu, s.t. sama programmi ei või saada kahe erineva derivatsioonipuu abil. Programmikäsu või lõigu tähenduse määrab just derivatsioonipuu, seega ühesus on oluline, kuna see tagab programmi ühese tähenduse, semantika.
Aritmeetilise avaldise "otse"-defineerimine
avaldis  avaldis op
avaldis | arv
avaldis op
avaldis | arv
op  + | - | * | /
+ | - | * | /
Mitmesus on tavaliselt põhjustatud informatsiooni puudumisest
grammatika mitteterminalide süsteemis. Mitteterminalid on grammatika
poolt kujutatava struktuuri alamosad, üldmõisted, mis võtavad kokku
mingi alamaosa. Matemaatilist avaldist ei kirjeldata koolimatemaatikas
nii lihtsalt nagu ülal: avaldis  avaldis op avaldis. Selline kirjeldus ei
anna informatsiooni matemaatiliste operatsioonide prioriteetidest:
korrutamine-jagamine on kõrgema prioriteediga ja tulevad sooritada enne
kui liitmine-lahutamine. Sellepärast kirjeldatakse koolimatemaatikas
matemaatiline avaldis kui hulkliige, mis koosneb üksliigetest;
üksliikmed koosnevad korrutamiste-jagamistega seotud arvudest.
Alammõiste üksliige lisab
avaldise kirjeldusse puuduva informatsiooni ja teeb selle üheseks:
avaldis op avaldis. Selline kirjeldus ei
anna informatsiooni matemaatiliste operatsioonide prioriteetidest:
korrutamine-jagamine on kõrgema prioriteediga ja tulevad sooritada enne
kui liitmine-lahutamine. Sellepärast kirjeldatakse koolimatemaatikas
matemaatiline avaldis kui hulkliige, mis koosneb üksliigetest;
üksliikmed koosnevad korrutamiste-jagamistega seotud arvudest.
Alammõiste üksliige lisab
avaldise kirjeldusse puuduva informatsiooni ja teeb selle üheseks:
avaldis  üksliige | avaldis + üksliige |
avaldis - üksliige
üksliige | avaldis + üksliige |
avaldis - üksliige
üksliige  arv | üksliige * arv | üksliige /
arv
arv | üksliige * arv | üksliige /
arv
Sellega ekvivalentne on veidi "teaduslikum" grammatika:
avaldis  üksliige | avaldis add_op üksliige
üksliige | avaldis add_op üksliige
üksliige  arv | üksliige mult_op arv
arv | üksliige mult_op arv
add_op  + | -
+ | -
mult_op  * | /
* | /
Klassikaline mitmese grammatika näide on if-lause ilma lõpetava (sulgeva) konstruktioonita, mis täpselt näitaks, kus then (ja else) järel täidetavad käsud lõpevad. Näiteks selline tingimuslause kirjeldamine (sellist skeemi kasutati esimeses FORTRAN-is ja Algol-is) on puuduliku infoga:
programm  käsk | käsk
programm
käsk | käsk
programm
käsk  omistamine | tingimuskäsk
omistamine | tingimuskäsk
omistamine  identifikaator = avaldis
identifikaator = avaldis
tingimuskäsk  IF tingimus THEN programm
IF tingimus THEN programm
| IF tingimus THEN programm ELSE programm
Selle grammatika järgi saab kahte sisestatud if-lauset
IF a>b THEN IF c<d THEN x := 1 ELSE x := 0
tõlgendada kahel viisil (sisestatud osa on võetud sulgudesse): kas nii IF a>b THEN (IF c<d THEN x := 1 ELSE x := 0)
IF a>b THEN (IF c<d THEN x := 1 ELSE x := 0)
 IF a>b THEN (IF c<d THEN x := 1) ELSE x := 0
IF a>b THEN (IF c<d THEN x := 1) ELSE x := 0
See tähendab, et vastaval programmilõigul on kaks erinevat semantikat. Kui enne selle if-konstruktsiooni täitmist näiteks x = 2 ja a=1, b=0, c=3, d=2, saame pärast if-lausete täitmist esimese tõlgenduse järgi x = 0, aga teise tõlgenduse järgi x = 2.
Kaasaegsetes programmeerimiskeeltes kasutatakse sellise konstruktsiooni sulgemiseks spetsiaalset võtmesõna, näit ENDIF, then- ja else-osa tegemist eraldajatega piiratud blokiks (nagu C-s) või reataannet (nagu keeles Python).
Kui programmerimiskeele grammatika on mitmene (seda juhtub uut programmerimiskeelt defineerides sageli), tuleb see enne praktilist kasutamist (s.t. enne seda, kui selle põhjal koostatakse translaator) tingimata teisendada üheseks. See teisendus ei ole algoritmiseeritav, s.t. ei ole võimalik koostada programmi, mis teisendaks mitmese grammatika üheseks (s.t. vastav probleem on mittelahenduv).
Kui leksika- või süntaksianalüsaatorit genereeriv programm (Flex, Bison, Antlr jne) teatab konfliktist, on põhjuseks enamasti alati sisestatud grammatika mitmesus. Näiteks definitsioon
programm  käsk |
programm programm
käsk |
programm programm
käsk  omistamine |tingimuskäsk
omistamine |tingimuskäsk
 programm programm arendades
järgmisel sammul esimest mitteterminali programm
või arendades teist mitteterminali programm.
programm programm arendades
järgmisel sammul esimest mitteterminali programm
või arendades teist mitteterminali programm.
Mitmene on ka järgnev kirjeldus:
exp  Term | exp + term | exp - term
Term | exp + term | exp - term
term  prim | prim * term | prim / term
prim | prim * term | prim / term
prim  IDENT | CONST | funct
IDENT | CONST | funct
funct  IDENT(args) | IDENT /* argumentideta
funktsioon */
IDENT(args) | IDENT /* argumentideta
funktsioon */
Selle järgi võib vaid ühest identifikaatorist koosnevat avaldist
tõlgendada nii identifikaatorina: exp  prim
prim  IDENT
kui ka funktsiooni nimena: exp
IDENT
kui ka funktsiooni nimena: exp  prim
prim  funct
funct  IDENT. Sellepärast nõutaksegi enamuses
programmeerimiskeeltes, et funktsiooni tähistuses peavad pärast
identifikaatorit kindlasti olema sulud ja identifikaatori ja sulgude
vahel ei või olla tühikuid - tühiku järel algavaid sulge võivad
skanner/süntaksianalüsaator tõlgendada sulgudesse võetud avaldisena.
IDENT. Sellepärast nõutaksegi enamuses
programmeerimiskeeltes, et funktsiooni tähistuses peavad pärast
identifikaatorit kindlasti olema sulud ja identifikaatori ja sulgude
vahel ei või olla tühikuid - tühiku järel algavaid sulge võivad
skanner/süntaksianalüsaator tõlgendada sulgudesse võetud avaldisena.
Kindlasti teatavad Flex+Bison ja Antlr veast ka leksika/süntaksi kirjelduse puhul, milles esinevad read:
...
vektor  '<' ident '>'
'<' ident '>'
operaator  aritm_op | loogika_op
aritm_op | loogika_op
aritm_op  + | - | * | /
+ | - | * | /
loogika_op  = | /= | > | <
= | /= | > | <
...
if_lause  'if' tingimus 'then käsud 'endif'
'if' tingimus 'then käsud 'endif'
tingimus  expr loogika_op expr
expr loogika_op expr
...
andmestruktuur  IDENT | vect | struct
IDENT | vect | struct
...
Kui analüüsitavas tekstis esineb näiteks konstruktsioon < Andmed >, siis skanner teisendab selle lekseemide jadaks loog_op IDENT loog_op ja leksikaanalüsaator ei suuda enam leida vektori definitsiooni, sest märke < , > kasutatakse ülalesitatud kirjelduses mitteüheselt.
Loomulikes keeltes (inglise, eesti,...) esineb mitteühesus väga sageli. Kui mitteühesusi - võimalusi juttu/teksti erinevalt tõlgendada - poleks, siis vist poleks ka vaja kõige enammakstud elukutset - juriste ("väänavad paragrahve nii et vähe pole ...."). Mõnikord on üldse arusaamatu, miks inimesed siiski (mõnikord) üksteist mõistavad, ja kuidas (näiteks) lapsed õpivad üksteisest aru saama. Näiteks lausel "Kõik hobused ei suutnud takistust ületada" (tõlgitud eesti keelde artiklist Vincenzo Moscati and Andrea Gualmini, "More Facts that Isomorphism Cannot Explain") on (vähemalt) kaks/rohkem? erinevat tõlgendust, sõltuvalt sellest, millele eitus "ei" on rakendatud; predikaatloogika modifitseeritud kirjaviisis oleks tõlgendused:
kõik hobused (ei (takistus.yletama()) //s.t.
hobused ei suutnud, aga (näiteks) elevandid suutsid
ei(kõik hobused) (takistus.yletama() ) //s.t. kõik ei suutnud (seda)
takistust ületada, aga mõni (võibolla) siiski sai sellest takistrusest
üle
kõik hobused ( (ei (takistus)).yletama() ) // kõik hobused SEDA
takistust ei ületanud, aga ületasid siiski mõne teise takistuse (mõned)
Kui inimeste käitumine põhineks (ainult) loogikal, oleks eelneva
näite põhjal selge, miks näiteks muidu täiesti ratsionaalsed/mõistusega
inimesed ei saa üksteisest aru - vt. Eesti parteide omavahelisest
kaklemisest kuni maailmasõdadeni. Kahjuks juhivad inimeste käitumist
veel palju rohkem isiklikud/kasusaamise/partei-riigipoliitelised jõud,
seega sageli on täiesti arusaamatu, miks miski üldse toimib. Ja
sellepärast juhtubki, et "tahtsime kõige paremat - 'eesti maailma viie
rikkama riigi hulka!!!', aga välja tuli nagu alati ... või veel palju
halvemini...".
Zhitt happenes, nagu tõdes kunagi kaheksakümnendatel Priit Pärn oma
kuulsas karikatuuris.
Ja loogika on ju vaid (inimeste endi poolt loodud) abstraktsioon, s.t. matemaatiline mudel sellest, kuidas me (inimesed) arutleme. Kuid kõiki reaalsuse protsesse saab abstraheerida väga mitmel viisil, sest ükski abstraktsioon ei kirjelda ühtki protsessi 100%-lise täpsusega - antiikmaailmas olid väga ebamäärased ettekujutused selle kohta, misk õunad kukuvad õunapuu alla, Newton sai juba millesti aru, siis esitas Einstein, et asi on palju keerulisem; praegu ei ole füüsikud ka Einsteini teooriaga rahul ("stringid" jms); Darvini evolutsiooniteooriat ei ole tunnustanud suur osa USA elanikes, kes väidavad "see kõik on siiski liiga keeruline, et see oleks võinud ise tekkida... selle pidi keegi looma" (creationism).
I II III IV V VI VII VIII IX X
Järgnev grammatika genereerib komaga eraldatud rooma numbrite jadasid:
Roman  Number ( ","
Number )*
Number ( ","
Number )*
Number  StartI | StartV | StartX
StartI | StartV | StartX
StartI  "I" ( "V" | "X" | [ "I" [ "I" ] ] )
"I" ( "V" | "X" | [ "I" [ "I" ] ] )
StartV  "V" [ "I" ] [ "I" ] [ "I" ]
"V" [ "I" ] [ "I" ] [ "I" ]
StartX  "X"
"X"
Kas see grammatika on ühene ? Kui ei, siis koosta ekvivalentne ühene grammatika!
programm  | käsk
programm
| käsk
programm
käsk  |omistamine | if | tsykkel
|omistamine | if | tsykkel
on ühene (mõlemad produktsioonid algavad tühja alternatiiviga)? Kui ei, siis koosta ekvivalentne ühene grammatika.
loogiline  True | False
| loogiline AND loogiline | loogiline OR loogiline
True | False
| loogiline AND loogiline | loogiline OR loogiline
on ühene? Kui ei, siis koosta ekvivalentne ühene grammatika.
name  simple_name |
indexed_component | slice
simple_name |
indexed_component | slice
simple_name  identifier
identifier
indexed_component  prefix(expression
{,expression})
prefix(expression
{,expression})
prefix  name | function_call
name | function_call
slice  prefix(discrete_range)
prefix(discrete_range)
discrete_range  subtype_indication | range
subtype_indication | range
range  range_attribute |
expression..expression
range_attribute |
expression..expression
range_attribute  type_name'attribute
type_name'attribute
type_name  Ident
Ident
attribute  Ident
Ident
subtype_indication  type_mark
type_mark
type_mark  Ident
Ident
expression  relation relop relation
relation relop relation
relop  and | or
| xor | and
then | or else
and | or
| xor | and
then | or else
relation  simple_expression |
[relational_operator simple_expression]
simple_expression |
[relational_operator simple_expression]
relational_operator  = | /= | < | <=
| > | >=
= | /= | < | <=
| > | >=
simple_expression  term {addop term}
term {addop term}
addop  + | - | &
+ | - | &
term  factor {multop factor}
factor {multop factor}
factor  name
name
Leia selles grammatikas (vähemalt) kaks mitmeselt kirjeldatud objekti; ülaltoodud produktsioonide paremates pooltes sümbolid { } (kordub 0,1,2,... korda) ja [ ] (kas on või pole) on grammatika metasümbolid, kuid ( ) , . ' Ident on terminalid.
namespace-name  original-namespace-name | class-name
original-namespace-name | class-name
original-namespace-name  namespace-alias
namespace-alias
namespace-alias  identifier
identifier
class-name  identifier | template-name
identifier | template-name
template-name  identifier
identifier
sentence ::= expression
expression ::= term | expression + term
term ::= identifier | term * identifier | expression
identifier ::= X | Y | Z
floatnumber  pointfloat | exponentfloat
pointfloat | exponentfloat
pointfloat  [intpart] fraction | intpart "."
[intpart] fraction | intpart "."
exponentfloat  (intpart | pointfloat)
exponent
(intpart | pointfloat)
exponent
intpart  digit+
digit+
fraction  "." digit+
"." digit+
exponent  ("e" | "E") ["+" | "-"] digit+
("e" | "E") ["+" | "-"] digit+
digit  [0..9]
[0..9]
slicing  simple_slicing | extended_slicing
simple_slicing | extended_slicing
simple_slicing  identifier "[" short_slice
"]"
identifier "[" short_slice
"]"
extended_slicing  primary "[" slice_list
"]"
primary "[" slice_list
"]"
slice_list  slice_item ("," slice_item)*
[","]
slice_item ("," slice_item)*
[","]
slice_item  expression | proper_slice
expression | proper_slice
proper_slice  short_slice | long_slice
short_slice | long_slice
short_slice  [lower_bound] ":" [upper_bound]
[lower_bound] ":" [upper_bound]
long_slice  short_slice ":" [stride]
short_slice ":" [stride]
lower_bound  expression
expression
upper_bound  expression
expression
stride  expression
expression
primary  atom |
attributeref
atom |
attributeref
attributeref  primary "." identifier
primary "." identifier
atom  identifier | literal
identifier | literal
literal  stringliteral | integer
stringliteral | integer
stringliteral  [stringprefix](shortstring | longstring)
[stringprefix](shortstring | longstring)
stringprefix  "r" | "u" | "ur" | "R" | "U"
| "UR" | "Ur" | "uR"
"r" | "u" | "ur" | "R" | "U"
| "UR" | "Ur" | "uR"
shortstring  "'" shortstringitem* "'"
| '"' shortstringitem* '"'
"'" shortstringitem* "'"
| '"' shortstringitem* '"'
longstring  "'''" longstringitem* "'''"
| '"""' longstringitem* '"""'
"'''" longstringitem* "'''"
| '"""' longstringitem* '"""'
shortstringitem  shortstringchar | escapeseq
shortstringchar | escapeseq
longstringitem  longstringchar | escapeseq
longstringchar | escapeseq
shortstringchar  <any ASCII character
except "\" or newline or the quote>
<any ASCII character
except "\" or newline or the quote>
longstringchar  <any ASCII character
except "\">
<any ASCII character
except "\">
escapeseq  "\" <any ASCII character>
"\" <any ASCII character>
"String literals can be enclosed in matching single quotes '...' or double quotes "...". They can also
be enclosed in matching groups of three single or double quotes (these
are generally referred to as triple-quoted
strings). The backslash \
character is used to escape characters that otherwise have a special
meaning, such
as newline, backslash itself, or the quote character. String literals
may optionally be prefixed with a letter 'r'
or 'R'; such strings are called
raw strings and use different rules for interpreting backslash escape
sequences. In triple-quoted strings, unescaped newlines and quotes are
allowed (and are retained), except that three unescaped
quotes in a row terminate the string. (A “quote” is the character used
to open the string, i.e. either '
or ".)
Unless an 'r' or 'R' prefix is present, escape sequences
in strings are interpreted according to rules similar to those
used by Standard C. The recognized escape sequences are:
\\
(Backslash \)
\’ (Single
quote ')
\" (Double
quote ")
\n (ASCII
Linefeed LF)"
 ©2004-2013 Jaak Henno
©2004-2013 Jaak Henno