Kui keerukas on Nim?

Eelmises paragrahvis kirjeldatud mängu Nim käiguvaliku algoritm:
- otsi käik, mille järel seis poleks enam mingil juhul võidetav (ükskõik kuimitu vastane ka võtaks)
on tegelikult kõigi võimalike antud seisust järgneda võivate seisude (seisude puu) läbivaatamine: et otsustada, kas antud seisule järgnev seis on mittevõidetav, peab samal viisil kontrollima sellele järgneda võivaid seise jne kuni jõutakse seisuni, kus laual enam pole tikke. Täielikud läbivaatused on alati kahtlased, sest siin väga sageli variantide arv hakkab plahvatuslikult kasvama (nn eksponentsiaalne keerukuse hüpe) ja ka hea arvuti muutub väga aeglaseks - ta ei suuda enam kõiki variante kiiresti läbi vaadata.
Laseme Prologil hinnata, kui palju variante ta peab mingi seisu võidetavuse määramiseks läbi vaatama. Seisu võidetavuse määramine taandub lõpuks alati lauseni
võiduseis(0).
jõudmist. Sinna jõudmiseks peab valima käike, s.t. käivitama predikaadi lubatud mingi lause:
lubatud(1).
lubatud(2).
Püüame hinnata, mitu korda (maksimaalselt) võib vaja minna kontrollida predikaadi lubatud lauseid.
Kui laual tikke enam pole (s.t. Seis = 0), siis kontrollide arv on 0. Kui laual on 1 tikk, siis (predikaadi lubatud lausete praeguse järjekorra juures) tehakse 1 kontroll; kui aga laual on 2 tikku, läheb tarvis 2 kontrolli, sest esimesena kontrollitakse lubatud(1) ja see ei õnnestu. Kui predikaadi lubatud lausete järjekord muuta vastupidiseks, siis tehakse kaks kontrolli juhul Seis=1. Kui predikaadi kontrolle(Seis,Kontrolle) teine argument on kontrollide arv, siis
kontrolle(1,1):-!.
kontrolle(2,2):-!.
ja predikaatide võidetav, pole_võidetav kirjelduse põhjal
võidetav(Seis,Käik) :-
lubatud(Käik),
Seis1 is Seis - Käik,
võiduseis(Seis1),
!.
võidetav(Seis,Käik) :-
lubatud(Käik),
Seis1 is Seis - Käik,
pole_võidetav(Seis1).
pole_võidetav(Seis) :-
Seis > 2,
Seis1 is Seis - 1,
Seis2 is Seis - 2,
võidetav(Seis1,_),
võidetav(Seis2,_).
kirjelduste põhjal on selge, et
kontrolle(Seis,N):-
Seis1 is Seis - 1,
Seis2 is Seis - 2,
kontrolle(Seis1,N1),
kontrolle(Seis2,N2),
N is 2*N1 + 2*N2 + 2 .
- predikaadi võidetav esimeses lauses tehakse 2 kontrolli (viimane liidetav 2), teises taandatakse kontroll 2 korda (halvimal juhul tuleb kontrollida nii lubatud(1) kui ka lubatud(2) ) ja predikaadis pole_võidetav taandatakse kontrollide arv kahe seisu läbivaatamisele - nii ühe kui ka kahe võrra väiksema tikkude arvuga.
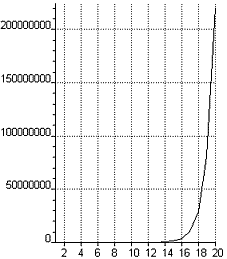
Funktsioonid, mille avaldises esineb uuesti sama funktsioon (s.t. rekursiivsed funktsioonid), tavaliselt kasvavad väga kiiresti. Kontrollime:
?- kontrolle(5,N).
N = 62
?- kontrolle(10,N).
N = 9514
?- kontrolle(20,N). N = 220436138
- on selge, et ka heas arvutis Prolog muutub selle algoritmi põhjal mängides väga aeglaseks (tegelikult on olemas väga lihtne algoritm - vastase ette peab jätma kolmega jaguva arvu tikke). Kõrvaloleval joonisel on funktsiooni kontrolle(X,Y) graafik, mis on saadud SWI-Prologi graafikasüsteemi abil; allpool on vastav programm:
:- use_module(library('plot/plotter')).
:- use_module(library(autowin)).

kontrolle(1,1):-!.
kontrolle(2,2):-!.
kontrolle(Seis,N):-
Seis1 is Seis - 1,
Seis2 is Seis - 2,
kontrolle(Seis1,N1),
kontrolle(Seis2,N2),
N is 2*N1 + 2*N2 + 2,!.

plot_function :-
To is 20,
PlotStep is 1,
Step is 2,
new(W, auto_sized_picture('Plotter demo')),
send(W, display, new(P, plotter)),
send(P, axis, new(X, plot_axis(x, 1, To, Step, 200))),
send(P, axis, plot_axis(y, 0, 225000000, @default, 300)),
send(X, format, '%i'),
send(P, graph, new(G, plot_graph)),
plot_function(1, To, PlotStep, Template, G),
send(W, open).

plot_function(X, To, _, _, _) :-
X > To, !.
plot_function(X, To, Step, Template, G) :-
kontrolle(X,Y),
send(G, append, X, Y),
NewX is X + Step,
plot_function(NewX, To, Step, Template, G).

Ülesandeid:
1. Ylesande tekst

Küsimused, probleemid: ©2004 Jaak Henno