Trips-traps-trull ja minimax

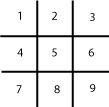
Mitmesugused mängud on alati kõitnud tehisintellekti uurijaid, sest just mänguprogrammide puhul on väga ilmne, kas programm on arukas või ei. Järgnev trips-traps-trulli mängiv programm kasutab oma käigu valikuks üsna lihtsat algoritmi, kuid mängib (peaaegu) optimaalselt, s.t. kui arvuti alustab, siis ta kunagi ei kaota.
Mäng algab mängulaua tähistuse selgitamisega; seejärel küsib arvuti, kumb alustab (vastata tuleb a või i , vastuse lõpus peab olema punkt - muidu prediaat read ei loe vastust lõpetatuks; alustamise võib lasta ka arvutil loosida predikaadiga random ). Olenevalt inimese vastusest käivitatakse kas arvuti käiku arvutav predikaat arvuti_käik või inimese käiku ootav predikaat inimese_käik; mõlema predikaadi argumentideks on kolm nimistut: arvuti poolt märgitud ruudud, inimese poolt märgitud ruudud ja veel vabad ruudud:

mäng :-
write('Edaspidi märgi ruudud numbritega:'),
nl,
nl,
joonista_algseis,
nl,
write('Kumb algab (a/i)?'),
read(Vastus),
(Vastus = a , ! , arvuti_käik([],[],[1,2,3,4,5,6,7,8,9]) ;
inimese_käik([],[],[1,2,3,4,5,6,7,8,9])).

Mänguseisu joonistamisel määrab ruudule joonistatava märgi predikaat märk . Joonistada tuleb X , kui ruut on inimese poolt märgistatud ruutude nimistus ja O , kui arvuti poolt joonistatud ruutude nimistus; kui ruut ei esine kummaski nimistus, jääb ta tühjaks. Algseisu joonistamise ajal aga tuleb igasse ruutu kirjutada ruudu järjekorranumber. Et seda saavutada, lisatakse (primitiivi asserta abil) algseisu joonistamise ajaks predikaadi märk kirjelduses esimeseks lause, mis tagab, et ruudu märk on selle ruudu järjekorranumber; niipea kui algseis on joonistatud, vastav lause eemaldatakse Prologi primitiiviga retract :

joonista_algseis :-
asserta(märk(N,_,_,N)),
joonista_seis([],[]),
retract(märk(N,_,_,N)).

joonista_seis(Arvuti,Inimene) :-
sirge(5,' '),
joonista_rida(1,Arvuti,Inimene),
nl,
sirge(5,' '),
sirge(10,-),
nl,
sirge(5,' '),
joonista_rida(2,Arvuti,Inimene),
nl,
sirge(5,' '),
sirge(10,-),
nl,
sirge(5,' '),
joonista_rida(3,Arvuti,Inimene),
nl.

märk(N,Arvuti,Inimene,'X') :-
member(N,Arvuti) , !.
märk(N,Arvuti,Inimene,'O') :-
member(N,Inimene) , !.

märk(_,_,_,' ').

joonista_rida(N,Arvuti,Inimene) :-
N1 is 3 * (N - 1) + 1,
märk(N1,Arvuti,Inimene,märk1),
write(märk1),
write(' I '),
N2 is N1 + 1,
märk(N2,Arvuti,Inimene,märk2),
write(märk2),
write(' I '),
N3 is N2 + 1,
märk(N3,Arvuti,Inimene,märk3),
write(märk3).

Predikaat sirge kirjutab antud arvu märke:

sirge(0,_) :-
!.

sirge(Pikkus,märk) :-
write(märk),
Pikkus1 is Pikkus - 1,
sirge(Pikkus1,märk).

Nii arvuti kui ka inimese käigu sooritamisel kontrollitakse, kas antud seisus üldse tasub jätkata (leidub veel mõni sirge, millel ei ole mõlema osavõtja märke). Süsteemipredikaat delete leiab nimistu, mis saadakse predikaadi esimesee argumendina olevast nimistust, kui sellest eemaldada teise argumendina olev ruut: :

inimese_käik(Arvuti,Inimene,Vabad) :-
kontrolli_viik(Arvuti,Inimene,Vabad).

inimese_käik(Arvuti,Inimene,Vabad) :-
write('Sinu käik, kirjuta selle ruudu number, kuhu tahad märgi!'),
nl,
nl,
read(Käik),
kontrolli_käik(Arvuti, Inimene, Vabad, Käik).

kontrolli_käik(Arvuti, Inimene, Vabad, Käik):-
member(Käik,Vabad) ,
! ,
delete(Vabad,Käik,Vahe) ,
arvuti_käik(Arvuti,[käik|Inimene],Vahe)

kontrolli_käik(Arvuti, Inimene, Vabad, _):-
write('See käik ei ole lubatud!') ,
nl ,
inimese_käik(Arvuti,Inimene,Vabad).

arvuti_käik(Arvuti,Inimene,Vabad) :-
võidab(Inimene),
write('õnnitlen, võitsid!'),
nl.

arvuti_käik(Arvuti,Inimene,Vabad) :-
kontrolli_viik(Arvuti,Inimene,Vabad).

arvuti_käik(Arvuti,Inimene,Vabad) :-
käik(Arvuti,Inimene,Vabad,Käik),
write('Rist ruudule '),
write(Käik),
nl,
nl,
joonista_seis([Käik|Arvuti],Inimene),
nl,
kontrolli_voit(Arvuti, Inimene, Vabad, Käik).

kontrolli_voit(Arvuti, Inimene, Vabad, Käik):-
võidab([Käik|Arvuti]) , ! , write('Võitsin!') , nl.
kontrolli_voit(Arvuti, Inimene, Vabad, Käik):-
vahe(Käik,Vabad,Vahe) ,
inimese_käik([Käik|Arvuti],Inimene,Vahe).

Mängu ei ole enam mõtet jätkata, kui kumbki ei suuda kõigi veel vabade ruutude täitmisel oma märkidega mängu võita. Sellepärast lisatakse viigi kontrolliks algul arvuti poolt täidetud ruutudele kõik vabad ruudu ja kontrollitakse, et saadud seis ei ole võiduseis, siis korratakse sama inimese poolt täidetud ruutude nimistuga:

kontrolli_viik(Arvuti,Inimene,Vabad) :-
append(Arvuti,Vabad,Ruudud1),
not võidab(Ruudud1),
append(Inimene,Vabad,Ruudud2),
not võidab(Ruudud2),
write('See mäng on viik'),
nl.

Ruutude nimistu on võiduseis (sellele mängijale, kumma ruudud need on), kui selles esinevad ühe sirge kõik ruudud:

võidab(Ruudud) :-
sirgeid(Ruudud,Arv),
Arv > 0.

Ruutude nimistus esinevate sirgete arvu määrab predikaat sirgeid Prologi süsteemipredikaadi findall abil; see kogub kõik tingimust (sirge(S),subset(S,Ruudud)) täitvad muutuja S väärtused nimistuks Sirged; Swi-Prologi süsteemipredikaat subset(Subset,Set) kontrollib, kas esimese nimistu Subset kõik elemendid esinevad ka teises nimistus Set:

sirgeid(Ruudud,Arv) :-
findall(S,(sirge(S),subset(S,Ruudud)),Sirged),
length(Sirged,Arv).

Arvuti poolt järgmisena täidetava ruudu arvutab predikaat käik . Kõige enne püüab see leida ruudu, mille täitmisel arvuti kohe võidaks; kui sellist ei leidu, otsitakse predikaadi käik teises lauses ruutu, mille täitmisel võiks inimene järgmisel käigul võita; kui sellist ruutu ka ei leidu, otsitakse vabadest ruutudest parim:

käik(Arvuti,Inimene,Vabad,Ruut) :-
member(Ruut,Vabad),
võidab([Ruut|Arvuti]).
käik(Arvuti,Inimene,Vabad,Ruut) :-
member(Ruut,Vabad),
võidab([Ruut|Inimene]).
käik(Arvuti,Inimene,Vabad,Ruut) :-
parim(Arvuti,Inimene,Vabad,Ruut).

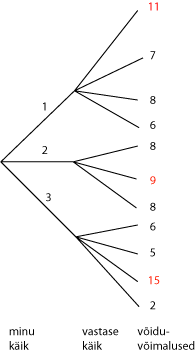Ruut on parim, kui sellesse ruutu oma märgi tegemine kõige enam tõstab arvuti võiduvõimalusi (sellise "parima" ruudu otsimine teebki programmi intelligentseks!). Täpsemini: kui antud ruudu märkimise (s.t. kasutaja käigu) järel vastane teeks (enda jaoks) parima käigu (mis annab talle maksimaalse võiduvõimaluse), siis tuleb valida selline käik, mis minimiseerib selle vastase maksimaalse võiduvõimaluse (vastase järgmise käigu järel). See on nn minimax printsiip ja seda kasutatakse edukalt paljudes mänguprogrammides; keerukamates mängudes tuleb vaid "ette vaadata" rohkem käike (siin vaadatakse vaid vastase järgmist käiku). Näiteks kõrvalolevas seisus tuleks valida käik 2: see minimiseerib vastase parimate võimaluste vektori (11, 9, 15).

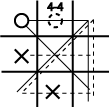Võiduvõimalused arvutatakse järgmiselt: algul arvutatakse minu (s.t. arvuti) potentsiaalne sirgete arv antud seisus, s.t. sirgete arv, mille arvuti saab, kui ta täidaks kõik veel vabad ruudud oma märkidega; siis arvutatakse samal viisil inimese potentsiaalsete sirgete arv; arvuti võiduvõimalused saadakse esimesest arvust teise lahutamisel (kellel on rohkem võimalusi sirgete saamiseks, see arvatavasti ka saab esimese sirge, s.t. võidab mängu). Näiteks kõrvalolevas seisus oleks arvuti (ring) jaoks ruudu 2 täitmisel võiduvõimaluste arv 0: selle täitmisel oleks tal 4 (potentsiaalset) võimalust sirge saamiseks, vastasmängijal (rist) ka 4; parim käik on see ruut, mille täitmine maksimiseerib võiduvõimaluste arvu (siin ruut 5, tsenter: võiduvõimaluste arv oleks 4-2 = 2):

parim(Arvuti,Inimene,Vabad,Ruut) :-
findall([R,Punktid],
(member(R,Vabad) ,
ruudu_Punktid(Arvuti,Inimene,Vabad,R,Punktid)),
PunktiRuudud),
kõrgeim(Ruut,Punktid,PunktiRuudud).

ruudu_Punktid(Arvuti,Inimene,Vabad,Ruut,Punktid) :-
vahe(Ruut,Vabad,Vahe),
seis([Ruut|Arvuti],Inimene,Vahe,Punktid).

kõrgeim(Ruut,Punktid,[[Ruut,Punktid]]) :-
!.

kõrgeim(Ruut,Punktid,[[R1,P1]|Ruudud]) :-
kõrgeim(R2,P2,Ruudud),
leia_max(R1, P1, R2, P2, Ruut, Punktid).

leia_max(R1, P1, R2, P2, R1, P1):-
P1 > P2 ,
! .

leia_max(R1, P1, R2, P2, R2, P2).

seis(Arvuti,Inimene,Vabad,Punktid) :-
append(Arvuti,Vabad,Arvutivoimalikud),
sirgeid(Arvutivoimalikud,Arvutisirged),
append(Inimene,Vabad,Inimesevoimalikud),
sirgeid(Inimesevoimalikud,Inimesesirged),
Punktid is Arvutisirged - Inimesesirged.

Ja lõpuks, millised ruudud moodustavad sirgeid:

sirge([1,2,3]).
sirge([4,5,6]).
sirge([7,8,9]).
sirge([1,4,7]).
sirge([2,5,8]).
sirge([3,6,9]).
sirge([1,5,9]).
sirge([3,5,7]).

Ülesandeid:

Eespoolkirjeldatud minimax-printsiipi saab kasutada paljude mängude jaoks "intelligentse" mänguprogrammi loomiseks. Tee programm, mis mängib mängu "Veski" (kahe mängija versiooni; (see on väga vana mäng ja reeglitel ja mängu nimel on palju versioone; üht võib näha näiteks lehel http://www.mastersgames.com/rules/morris-rules.htm ). Mängu reeglid on järgmised.

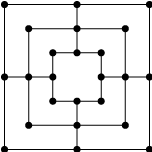
Mängu algul on kummalgi mängijal 9 mängunuppu; mängulaud (kõrvaloleval pildil) on tühi. Alustaja loositakse ja seejärel paigutavad mängijad kordamööda oma nuppe laua vabadele ringikestele. Eesmärgiks on moodustada "veski", s.t. 3 järjestikust oma nuppu ühel horisontaal- või vertikaalsirgel; sellise kujundi saamisel eemaldatakse mingi vastasmängija nupp. Eemaldada võib vaid sellise nupu, mis ei kuulu mingisse (vastase) "veskisse", kuid kui kõik vastase nupud kuuluvad mingisse "veskisse", võib eemaldada ükskõik millise tema nupu. Kui kõik nupud on lauale paigutatud, jätkub mäng oma nupu liigutamisega mööda sirget vabale naaberväljale. Kaotab see, kellel jääb järele < 3 nuppu või kes ei saa enam oma nuppe liigutada.

2. Minimax-printsiibi jaoks sobiv sihifunktsioon ei tarvitse olla keeruline - kuna arvuti suudab erinevaid versioone läbi vaadata tunduvalt effektiivsemalt kui inimene, annab (tavaliselt) ka lihtne funktsioon hea tulemuse.
Mäng Reversi (üks versioon) toimub 8x8 ruudust koosneval laual, kuhu mängijad kordamööda asetavad ühekaupa oma mängunuppe. Esimeste kahe käiguga tuleb täita mänguvälja keskel olev neljast ruudust koosnev ala. Seejärel võib paigutada oma nupu igale vabale ruudule, kui selle ruudu (paigutatud oma nupu) kõrval (kas horisontaal-, püst- või diagonaalsuunas) asetseb vastasmängija nupp ja selles suunas oleval sirgel asub (mingi arvu) vastasmängija nuppude järel oma nupp; nende kahe oma nupu vahel olevad vastasmängija nupud asendatakse seejärel oma nuppudega. Mäng jätkub kuni kas mängija kõik nupud on eemaldatud või mängija ei saa käigul olles enam käia.
Kuigi Reversi ruutude tähtsus on erinev (2x2 tsentriruutude hõivamine on kasulik, nurgas olevat nuppu ei ole vastasel enam võimalik lüüa jne), võib sihifunktsiooniks võtta näiteks kahe käigu järel laual olevate oma ja vastase nuppude arvu vahe; see lihtne funktsioon annab juba nii hea tulemuse, et inimesel on väga raske arvutit võita. Realiseeri Reversi programm selle sihifunktsiooni põhjal.

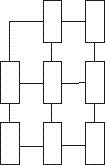
Reversi modifikatsioonis on mõlemal mängijal vaid kaks nuppu; mänguväljak võib olla ükskõik millise konfiguratsiooniga labürint. Algul asetavad mängijad oma nupud kordamööda ühekaupa mängulaua vabasse ruutu. Seejärel võivad nad käigul olles liigutada oma nuppu ruute ühendavat sirget mööda kõrvalolevale vabale ruudule; kes enam ei saa liikuda, on kaotanud, näiteks kõrvaloleval ruudustikul mängides võib alustaja (õige taktika korral) alati võita.

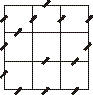
Mängulaud on n x n ruudustik (n > 2), mille ruudukeste külgeservi mängijad kordamööda läbi kriipsutavad, kuid mängija võib oma käigust (läbikriipsutamisest) ka loobuda. Kui mängija kriipsutab läbi ruudukese viimase külje, saab ta ruudukese endale ja peab veel ühe läbikriipsutuse tegema; võidab see, kes saab endale rohkem ruute. Näiteks kõrvaloleva 3 x 3 mängus saab käigul olev mängija järjest kaks vasaku ülanurga ruutu, kuid peab siis veel kusagil läbikriipsutuse tegema ja seejärel saab vastasmängija endale kõik ülejäänud ruudukesed.
Koosta mini-max printsiibil töötav programm n x n mängu mängimiseks (n väärtus leitakse mängu algul funktsiooni random abil, 2 < n < 10).

5. (mäng "neli reas") Mäng sarnaeb trips-traps trulliga, kuid ritta (vertikaal, horisontaal või diagonaalritta) peab saama neli oma nuppu; mängulaua suurus (10 > n > 4 ) sisestatakse mängu algul; keerukam modifikatsioon (sellist mängu saab osta paljudest mänguasjade kauplusest) - laud on mängimise ajal püsti ja mängijad sisestavad nuppe ülaservast, mis siis langevad vastavas veerus nii madalale kui saavad.

Küsimused, probleemid: