Loogiliste skeemide modelleerimine
Prologi abil on lihtne kontrollida loogiliste skeemide
tööd, s.t. millise seose sisendite-väljundite vahel skeem realiseerib.
Selgitame Prologile algul, kuidas töötavad köige lihtsamad skeemid:
eitus (ei-skeem), disjunktsioon (vöi) ja konjunktsioon (ja, predikaatide nimedena ei või
kasutada Prologi
reserveeritud sõnu not, and,
or); vastavate predikaatide
esimesed attribuudid on sisendid, viimane - väljund:
ei(0,1).
ei(1,0).
vöi(0, 0, 0).
vöi(0, 1, 1).
vöi(1, 0, 1).
vöi(1, 1, 1).
ja(0, 0, 0).
ja(0, 1, 0).
ja(1, 0, 0).
ja(1, 1, 1).
 Näiteks funktsiooni (X1 v X2) & X3 = X1X3 & X2X3 realiseerib predikaat
Näiteks funktsiooni (X1 v X2) & X3 = X1X3 & X2X3 realiseerib predikaat
vöi3(X1,X2,X3,Väljund) :-
vöi(X1, X2, Väljund1),
ja(Väljund1, X3, Väljund).
Sisendite Sisse1 ja Sisse2
summa mod 2 järgi 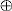 (nn. välistav ehk x-or summa, exclusive-or)
(nn. välistav ehk x-or summa, exclusive-or)
(Sisse1+Sisse2) mod2 = (ei(Sisse1)&Sisse2) v (Sisse1&ei(Sisse2))
määrab predikaat xor koos abipredikaadiga ei_Xja_Y:
xor(Sisse1,Sisse2,Väljund) :-
ei_X_ja_Y(Sisse1, Sisse2, Väljund11),
ei_X_ja_Y(Sisse2, Sisse1, Väljund12),
vöi(Väljund11, Väljund12, Väljund).
ei_X_ja_Y(Sisse1, Sisse2, Väljund) :-
ei(Sisse1, Väljund1),
ja(Väljund1, Sisse2, Väljund).
Olgu X1X2 kahekohaline kahendarv (X1 -
arvu esimene bit, X2 - teine bit). Kahe kahekohalise kahendarvu
X1X2 ja Y1Y2 kolmekohalise
summa S1S2S3 arvutab predikaat summa2.
Abipredikaat summa_ja_meeles teostab "tulba kujul" arvutamisel ühe püsttulba juures sooritatavad
operatsioonid: arvutab üksteise kohal olevate kahendkohtade ja eelmise koha liitmisel saadud ülekande
pöhjal summa kahendnumbri ja uue ülekande. Kui liidetavad on X,
Y, eelmine ülekanne C, uus
summanumber S ja uus ülekanne C1,
saadakse S ja C valemitega
S = X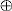 Y
Y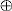 C, C1 = XY v XC v YC :
C, C1 = XY v XC v YC :
summa2(X1,X2,Y1,Y2,S1,S2,S3) :-
summa_ja_meeles(X2, Y2, 0, S3,C1),
summa_ja_meeles(X1, Y1, C1, S2, S1).
summa_ja_meeles(X, Y, C, S, C1) :-
summa(X, Y, C, S),
meeles(X, Y, C, C1).
meeles(X, Y, C, C1) :-
ja(X, Y, XjaY),
ja(X, C, XjaC),
ja(Y, C, YjaC),
vöi(XjaY, XjaC, Z),
vöi(Z,YjaC, C1).
summa(X, Y, C, Summa) :-
xor(X, Y, Xvöi1Y),
xor(C, Xvöi1Y, Xvöi1Yvöi1C),
ja(Y, C, YjaC),
ja(X, YjaC, XjaYjaC),
vöi(Xvöi1Yvöi1C, XjaYjaC, Summa).
Ülesandeid:
1.
Koosta predikaat
liida(X, Y, S), mis liidab kaks n-kohalist
kuitahes pikka kahendarvu
X ja
Y (lihtsam versioon: sama pikkusega, keerukam - liidetavate pikkused
võivad olla erinevad).
Kahendarvud on esitatud oma bittide nimistuna
(st. arv
100101 esitatakse kujul
[1,0,0,1,0,1]) ja
arvude
X ja
Y summa
S
esitatakse samal viisil (
S pikkus on ühe võrra suurem
pikema liidetava pikkusest).
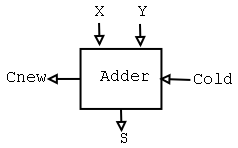
Kasuta alamskeemi, mis liidab kaks bitti
X,
Y ja eelmisese
ülekande
Cold ja saab tulemuseks summa biti
S ja
uue ülekande
Cnew (vt kõrvaloleval joonisel).
Kahe suvalise (sama) pikkusega bitijada
Xn...X2X1,
Yn...Y2Y1
liitmisel saadava bitijada
Sn+1Sn...S2S1 saab selle alamskeemi
abil arvutada alltoodud skeemiga, mida on (induktsiooniga liidetavate pikkuse järgi) lihtne teisendada Prologi predikaatideks.

2.
Eelnev ülesanne, kuid sisendid-väljund
esitatakse aatomitena, s.t. õigel kahendarvu kujul (bitid vasakult paremale järjekorras,
nagu kümnendsüsteemi arvude kirjutamisel) .
3.
Eelnev ülesanne, kus liita võib kuitahes mitu kahendarvu, s.t.
liitmispredikaadi esimene argument on nimistu liidetavatest; lihtsam - kõik liidetavad bitinimustud, nagu ülesandes 1;
keerukam - kõik liidetavad ja tulemus aatomid, õiges järjekorras (vasakult paremale, nagu kümnendsüsteemi arvude kirjutamisel) bitid.
Küsimused, probleemid:
 ©2004
Jaak Henno
©2004
Jaak Henno

 Näiteks funktsiooni (X1 v X2) & X3 = X1X3 & X2X3 realiseerib predikaat
Näiteks funktsiooni (X1 v X2) & X3 = X1X3 & X2X3 realiseerib predikaat
 Koosta predikaat liida(X, Y, S), mis liidab kaks n-kohalist
kuitahes pikka kahendarvu X ja Y (lihtsam versioon: sama pikkusega, keerukam - liidetavate pikkused
võivad olla erinevad).
Kahendarvud on esitatud oma bittide nimistuna
(st. arv 100101 esitatakse kujul [1,0,0,1,0,1]) ja
arvude X ja Y summa S
esitatakse samal viisil (S pikkus on ühe võrra suurem
pikema liidetava pikkusest).
Kasuta alamskeemi, mis liidab kaks bitti X, Y ja eelmisese
ülekande Cold ja saab tulemuseks summa biti S ja
uue ülekande Cnew (vt kõrvaloleval joonisel).
Kahe suvalise (sama) pikkusega bitijada Xn...X2X1, Yn...Y2Y1
liitmisel saadava bitijada Sn+1Sn...S2S1 saab selle alamskeemi
abil arvutada alltoodud skeemiga, mida on (induktsiooniga liidetavate pikkuse järgi) lihtne teisendada Prologi predikaatideks.
Koosta predikaat liida(X, Y, S), mis liidab kaks n-kohalist
kuitahes pikka kahendarvu X ja Y (lihtsam versioon: sama pikkusega, keerukam - liidetavate pikkused
võivad olla erinevad).
Kahendarvud on esitatud oma bittide nimistuna
(st. arv 100101 esitatakse kujul [1,0,0,1,0,1]) ja
arvude X ja Y summa S
esitatakse samal viisil (S pikkus on ühe võrra suurem
pikema liidetava pikkusest).
Kasuta alamskeemi, mis liidab kaks bitti X, Y ja eelmisese
ülekande Cold ja saab tulemuseks summa biti S ja
uue ülekande Cnew (vt kõrvaloleval joonisel).
Kahe suvalise (sama) pikkusega bitijada Xn...X2X1, Yn...Y2Y1
liitmisel saadava bitijada Sn+1Sn...S2S1 saab selle alamskeemi
abil arvutada alltoodud skeemiga, mida on (induktsiooniga liidetavate pikkuse järgi) lihtne teisendada Prologi predikaatideks.

 ©2004
Jaak Henno
©2004
Jaak Henno