Määratud integraal

Määratud integraal on kõverjoonelise trapetsi pindala; trapets moodustub integreerimisvahemiku otste, s.t. sirgete X=a ja X=b, sirge Y=0 (x-telg) ja integreeritava funktsiooni f(x) graafiku vahel. Integraali numbrilise väärtuse saamiseks asendatakse funktsiooni graafik (kõver) sirglõikudega, kõige lihsamal juhul vaid yhe sirglõiguga.

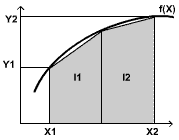Täpsema tulemuse saamiseks jagatakse integreerimisvahemik pooleks, arvutatakse integraali väärtused I1, I2 pooltel ja saadakse kogu integraal pindalate summana I = I1+I2. Et saada veel täpsemat tulemust, võib osade poolitamist jätkata; poolitamiste arvu nimetatakse integreerimismeetodi astmeks. Kuna integreerimismeetodi astme tõstmisel arvutusvead akumuleeruvad (liituvad), ei saa astme tõstmisega tulemust lõpmatuseni parandada. Õigete kümnendkohtade arvu tulemuses võib hinnata näiteks nii, et arvutatakse integraal kaks korda, tõstes teine kord meetodi järku ühe võrra; kokkulangevad kümnendkohad on kindlasti õiged.

funktsioon(X,Y) :-
Y is X * X.

integraal(X1,X2,1,I) :-
funktsioon(X1,Y1),
funktsioon(X2,Y2),
trapets(X1,Y1,X2,Y2,I).

integraal(X1,X2,N,I) :-
N > 1,
X is (X1 + X2) / 2,
N1 is N - 1,
integraal(X1,X,N1,I1),
integraal(X,X2,N1,I2),
I is I1 + I2.

integraal :-
write('Anna integreerimisvahemik: a= '),
read(A),
write('b= '),
read(B),
write('Integreerimismeetodi aste: '),
read(N),
integraal(A,B,N,I),
nl,
write('Tulemus: '),
write(I),
nl.

trapets(X1,Y1,X2,Y2,S) :-
H is (Y1 + Y2) / 2,
S is (X2 - X1) * H.

Ülesandeid:

1. Ülalkirjeldatud meetod on väga ebaeffektiivne. Kuna integreerimismeetodi järgu tõstmine suurendab Prologi alamülesannete arvu kaks korda, tekib näiteks kuuendat järku meetodi kasutamisel 2^6 = 64 alamülesannet ja isegi madala järguga meetod võib anda teate "Stack overflow".
"Prologilik" lähenemine oleks lõpprekusriive: algul arvutatakse meetodi järgu põhjal kõige lühema integreerimislõigu pikkus (selle lõigu pikkus, millel kasutatakse trapetsit) ja hakatakse siis nende trapetsite pindala vasakult-paremale järjest arvutama ja kokku liitma. Koosta lõpprekursiivne predikaat numbriliseks integreerimiseks.

Teha programm, mis arvutab määratud integrale ristkülikvalemi põhjal: esimest järku valemiga arvutades leitakse lõigu keskpunk ja asendatakse integraal ristkülikuga, mille kõrgus on võrdne integreeritava funktsiooni väärtusega lõigu keskpunktis; kõrgemat järku valem saadakse lõigu järk-järgulisel poolitamisel.

Küsimused, probleemid: