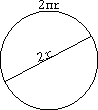Ridade summeerimine

Arv π on lõpmatu kümnendmurd:
π = 3.14159...
s.t. π (täpne) väärtus sisaldab lõpmata palju informatsiooni, seda ei ole võimalik esitada lõpliku pikkusega stringina. Kuid π-l on väga lihtne (lõplik) kirjeldus:
π on ringjoone ümbermõõdu ja läbimõõdu suhe.

Tundub, et siin on vastuolu: lõpmatu suurus on kirjeldatud lõpliku avaldisega?
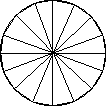Tegelikult sisaldab see lõplik avaldis mõiste, mis ei ole lõplik: "ringjoone ümbermõõt". Ringjoone ümbermõõt on suurus, millele läheneb ringjoone sisse joonestatud (korrapärase) hulknurga ümbermõõt hulknurga külgede arvu (piiramatul) suurendamisel, s.t. ringjoone ümbermõõt on määratud lõpmatu protsessi abil. Väljend "ringjoone ümbermõõt" on (lõpmatu) informatsiooni kompressioonivõte.

Paljud matemaatikas esinevad suurused (arv e) ja funktsioonid (sin, ln) on sellised, et nende täpset väärtust pole võimalik lõplikul viisil esitada. Nende väärtus saadakse mingi (lihtsa) arvutusprotsessi abil, mis korrates annab otsitava väärtuse üha täpsemalt ja täpsemalt.

Arvu π kümnendkohtade arvutamiseks esitas kuulus matemaatik ja loogik Leibniz valemi:
π = 4 x (1-1/3 + 1/5 - 1/7 + 1/9 ...)
Selle arvutamist on lihne kirjeldada Prologi predikaadina:

pii(N,Pii):-
summa(N,Summa),
Pii is 4 * Summa,
write('Pii = '),
write(Pii),
nl.

summa(1,1).
liidetav(N,Liidetav):-
paaritu(N),
Liidetav is 1 / (2 * N - 1).

liidetav(N,Liidetav):-
paaris(N),
Liidetav is - 1 / (2 * N - 1).

paaritu(N):-
X is N mod 2,
X = 1.

paaris(N):-
X is N mod 2,
X = 0.

Kahjuks koondub Leibnizi rida äärmiselt aeglaselt, isegi 500 rea liiget ei anna veel kaht õiget kümnendkohta (kui tulemus ümmardada kahe kohani pärast koma):

?- pii(500,P).
Pii = 3.13959

Märksa kiiremini koondub Vieta valem: 2/π = v(1/2)v((1+v(1/2))/2)v((1+v((1+v(1/2))/2))/2...
s.t. iga järgmine tegur T(N) = v((1 + T(N))/2).

tegur(1,Tegur):-
Tegur is sqrt(1 / 2),
!.
tegur(N,Tegur):-
N1 is N - 1,
tegur(N1,Eelmine),
Tegur is sqrt((1 + Eelmine) / 2).

korrutis(1,Korrutis):-
Korrutis is 1/sqrt(2),!.
korrutis(N,Korrutis):-
N1 is N - 1,
korrutis(N1,Korrutis1),
tegur(N,Tegur),
Korrutis is Korrutis1 * Tegur.

pii1(N,Pii):-
korrutis(N,Korrutis),
Pii is 2 / Korrutis,
write('Pii = '),
write(Pii),
nl.

See lõpmatu korrutis annab SWI-prologis kasutava tavaliste reaalarvude esitamise täpsuse (5 kohta peale koma) juba esimese kümne liikmega:

?- pii1(10,Pii).
Pii = 3.14159

Ülesandeid:

1. Koosta ülalesitatud arvutusprotseduuride jaoks lõpprekursiivsed predikaadid!

2. Lõpmatud avaldised esinevad ka rekursiivselt kirjeldatud pindalate arvutamisel. Järgnevas kujundite reas (nn Sierpinski vaip) saadakse iga järgnev esialgse kujundi küljepikkuse jagamisel kolmega ja selle asendamisel eelneva kujundi kõigisse (veel) valgetesse ruutudesse:

Millele läheneb järgneva kujundi (nn Sierpinski vaip) pindala ruutude arvu suurendamisel (ruudu küljepikkus on 1)?

Küsimused, probleemid: