
Kui lind otsustaks, et inimene on "looduse kroon" ja tahaks kevadel saada mune pesasse
"inimliku" tehnoloogiaga, siis peaks ta algul valmis treima tühja munakoore, siis segama kõrval valmis kollase täidise
ja lõpuks selle kuidagi koore sisse saama ja koore seejärel sulgema.
Loodus ei toimi nii nagu inimene: algul tehakse osad ja siis koostatakse tervik.
Loodus teeb kõiki asju korraga:
taimel kasvavad korraga juured, vars, lehed ja valmivad õienupud, lootel arenevad
samaaegselt kõik organid, elukeskkonna saastumine toimub korraga nii maal,
vees kui ka õhus jne. Ja paljud näiliselt keerukad struktuurid ja protsessid
põhinevad sageli väga lihtsatel algoritmidel, mida rakendatakse rekursiivselt
ja paralleelselt, kusjuures need algoritmid ise ei "tea", mis sellest kõigest
peab saama.
Nii arenevad kõik elusorganismid, lumekristallid jne jne. Sellisel "tootmisviisil" on palju eeliseid tööstusliku osadest kokku panemise meetodi suhtes ja see võimaldab täiesti uute omadustega materjalide ja konstruktsioonida valmistamist, sellepärast on viimasel ajal hakatud looduslike protsesside algoritmikat intensiivselt uurima, on tekkinud uus arvutiteaduse haru: bioinformaatika, looduslikke protsesse uuriv arvutus.
Esimesed bioinformaatika põhialgoritmid formuleeris juba 1968 a Charles Darwin ( areng toimub loodusliku valiku teel - see sai hiljem aluseks John H. Hollandi loodud geneetiliste algoritmidele). 1968 a. formaliseers Hollandi bioloog Aristid Lindenmayer taime struktuuri arengu kirjelduse nn Lindenmayeri süsteemide abil.
 Areng algab mingist väga lihtsast elementaarstruktuurist (rakust, oksaraost, veekristallist). Rakk paljuneb, s.t. ta asendatakse järgmisel
sammul mingi
uute rakkudega; need igaüks taas uutega jne. Iga rakk asendatakse teistest sõltumatult ja samaaegselt (paralleelselt),
kuid alati samu asendusreegleid kasutades. Loomulikult on kõigil tekkinud struktuuridel ka individuaalsed
parameetrid - asend kogu struktuuris, suurus (vanad oksaraod on pikemad) ja asendamisel võetakse neid arvesse (uued rakud tekkivad vana
asemele või juurde), kuid asendusreeglid on alati samad. Selliseid struktuure (fraktaale - struktuuri kõik väiksemad osad
sarnanevad kogu struktuuri osadega) on
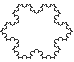
matemaatikud uurinud varemgi, näiteks kirjeldas Rootsi matemaatik Helge von Koch 1904 a nii
lumehelbe piirjoone tekkimist.
Areng algab mingist väga lihtsast elementaarstruktuurist (rakust, oksaraost, veekristallist). Rakk paljuneb, s.t. ta asendatakse järgmisel
sammul mingi
uute rakkudega; need igaüks taas uutega jne. Iga rakk asendatakse teistest sõltumatult ja samaaegselt (paralleelselt),
kuid alati samu asendusreegleid kasutades. Loomulikult on kõigil tekkinud struktuuridel ka individuaalsed
parameetrid - asend kogu struktuuris, suurus (vanad oksaraod on pikemad) ja asendamisel võetakse neid arvesse (uued rakud tekkivad vana
asemele või juurde), kuid asendusreeglid on alati samad. Selliseid struktuure (fraktaale - struktuuri kõik väiksemad osad
sarnanevad kogu struktuuri osadega) on
matemaatikud uurinud varemgi, näiteks kirjeldas Rootsi matemaatik Helge von Koch 1904 a nii
lumehelbe piirjoone tekkimist.
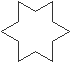
Olgu näiteks algstruktuur kolmnurk 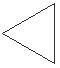
ja asendusreegel
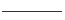 →
→ 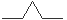 ,
st. siglõigu keskmine kolmandik asendatakse
"hambaga" (hamba suurus kohandatakse alati asendatava lõigu suurusega).
,
st. siglõigu keskmine kolmandik asendatakse
"hambaga" (hamba suurus kohandatakse alati asendatava lõigu suurusega).
 →
→
 →
→
 → ...
→ ... nn kilpkonnagraafika (Turtle Graphics, mille tegi tuntuks joonistamissüsteem Logo)
operatsioonidena. Kilpkonnagraafikas joonistatab kilpkonn, keda juhitakse
käskudega:
nn kilpkonnagraafika (Turtle Graphics, mille tegi tuntuks joonistamissüsteem Logo)
operatsioonidena. Kilpkonnagraafikas joonistatab kilpkonn, keda juhitakse
käskudega:Võttes a = 90°, algfiguuriks
f-f-f-f (ruut) ja
kasutades reeglit f ? f-f+ff-f-f+f
![]() →
→
![]()
saame algfiguurist pärast kahte
arengusammu nn Kochi kujundi  .
.
Lindenmayeri süsteemi reegli ja kujundeid on lihtne esitada XPCE-Prologi predikaatidena. Kirjeldame kilpkonnagraafika süsteemi jaoks uue klassi, kus on määratud kilpkonnagraafikas kasutatavad muutujad ja nende algväärtused; iga muutuja jaoks tuleb ka määrata, kas ta on sisend, väljund, või nii sisend kui ka väljund (both):
:- use_module(library(pce)).
:- pce_begin_class(drawing,class).
variable(x,int:=0,both).
variable(y,int:=0,both).
variable(angle,int:=0,both).
variable(pen,int:=1,both).
variable(color,string:='#000000',both).
variable(visible,int:=1,both).
:- pce_end_class.
:- free(@graphics).
:- pce_global(@graphics,new(window('Draw',size(800,600)))).
init :-
defaultcolors,
clearscr,
pendown(1).
quit:-
send(@graphics,destroy).
Kilpkonna asendi määramisel (setDraw) ja lugemisel (getDraw) on mõnikord tarvis peale põhimuutujate X,Y,Suund määrata ka muutujate Sulg (kui jäme on joonistamissule, joon; Sulg=0 - joont pole) ja Nähtav (kas kilpkonn on nähtav või mitte) väärtused, sellepärast on setDraw, getDraw kirjeldatud nii kolme, nelja kui ka viie muutujaga:
getDraw(X,Y,Suund,Sulg,Nähtav) :-
get(@myDrawing_class,x,X),
get(@myDrawing_class,y,Y),
get(@myDrawing_class,angle,Suund),
get(@myDrawing_class,pen,Sulg),
get(@myDrawing_class,visible,Nähtav).
getDraw(X,Y,Suund,Sulg) :-
get(@myDrawing_class,x,X),
get(@myDrawing_class,y,Y),
get(@myDrawing_class,angle,Suund),
get(@myDrawing_class,pen,Sulg).
getDraw(X,Y,Suund) :-
get(@myDrawing_class,x,X),
get(@myDrawing_class,y,Y),
get(@myDrawing_class,angle,Suund).
getColor(Color) :-
get(@myDrawing_class,color,Color).
forward(N) :-
getDraw(X,Y,Suund,Sulg),
rad(Suund,Rad),
X1 is round(X+N*cos(Rad)),
Y1 is round(Y+N*sin(Rad)),
setDraw(X1,Y1,Suund),
line(X,Y,X1,Y1,Sulg).
back(N) :-
getDraw(X,Y,Suund,Sulg),
rad(Suund,Rad),
X1 is round(X-N*cos(Rad)),
Y1 is round(Y-N*sin(Rad)),
setDraw(X1,Y1,Suund),
line(X,Y,X1,Y1,Sulg).
left(Suund) :-
getDraw(X,Y,CurrentAngle),
NewAngle is ((CurrentAngle+Suund) mod 360),
setDraw(X,Y,NewAngle).
right(Suund) :-
getDraw(X,Y,CurrentAngle),
NewAngle is ((CurrentAngle-Suund) mod 360),
setDraw(X,Y,NewAngle).
home :-
setDraw(0,0,90).
penup :-
send(@myDrawing_class,pen(0)).
pendown :-
send(@myDrawing_class,pen(1)).
pendown(N) :-
send(@myDrawing_class,pen(N)).
label(String) :-
getDraw(X,Y,Suund),
getColor(Color),
transf(X,Y,X1,Y1),
new(Text,text(String)),
send(Text,colour,Color),
send(@graphics,display(Text,point(X1,Y1))).
setx(X) :-
getDraw(CurrX,Y,Suund,Sulg),
line(CurrX,Y,X,Y,Sulg),
setDraw(X,Y,Suund). %,paintDraw.
sety(Y) :-
getDraw(X,CurrY,Suund,Sulg),
line(X,CurrY,X,Y,Sulg),
setDraw(X,Y,Suund).
setxy(X,Y) :-
getDraw(CurrX,CurrY,Suund,Sulg),
line(CurrX,CurrY,X,Y,Sulg),
setDraw(X,Y,Suund).
line(X0,Y0,X1,Y1) :-
transf(X0,Y0,X0v,Y0v),
transf(X1,Y1,X1v,Y1v),
new(Line,line(X0v,Y0v,X1v,Y1v)),
getColor(Color),send(Line,colour,Color),
get(@myDrawing_class,pen,N),
send(Line,pen,N),
send(@graphics,display(Line)).
line(X0,Y0,X1,Y1,N) :-
transf(X0,Y0,X0v,Y0v),
transf(X1,Y1,X1v,Y1v),
new(Line,line(X0v,Y0v,X1v,Y1v)),
getColor(Color),send(Line,colour,Color),
send(Line,pen,N),
send(@graphics,display(Line)).
ring(Diameeter) :- %joonistab praeguse asukoha ümber
ringjoone
new(Ring, circle(Diameeter)),
getDraw(X,Y,_,Sulg),
transf(X,Y,X1,Y1),
XR is X1-Diameeter/2, %Swi-Prologis on graafilise kujundi nullpunk ylemine
vasak nurk
YR is Y1 - Diameeter/2, %teisendame selle ringi keskele
getColor(Color),
send(Ring,pen,Sulg), %ringjoone paksus
send(Ring,colour,Color), %joone värv!
send(@graphics,display(Ring,point(XR,YR))).
ring(Diameeter,Värv) :- %joonistab värviga täidetud
ringjoone
new(Ring, circle(Diameeter)),
getDraw(X,Y,_,Sulg),
transf(X,Y,X1,Y1),
XR is X1 - Diameeter/2,
YR is Y1 - Diameeter/2,
getColor(Color),
send(Ring,pen,Sulg), %ringjoone paksus
send(Ring,colour,Color), %joone värv!
send(Ring, fill_pattern, Värv),
send(@graphics,display(Ring,point(XR,YR))).
defaultcolors :-
setpencolor('#000000'),
setbgcolor('#ffffff').
clearscr :-
send(@graphics,clear),
setDraw(0,0,90).
clean :-
send(@graphics,clear).
setpencolor(Color) :-
send(@myDrawing_class,color(Color)).
setbgcolor(Color) :-
send(@graphics,background(Color)).
Swi-Prolog-is on koordinaatide nullpunkt (nagu enamuses graafikasüstemides) akna vasakus ülanurgas; kilpkonnagraafika-stiilis joonistamisel teisendatakse koordinaatsüsteemi nii, et koordinaatide alguspunk asuks akna keskel; vaja on ka abipredikaate nurkade suuruse teisendamiskes kraadidest radiaanidesse ja vastupidi. Et ringi täitevärvi saaks määrata sõnaga (Swi-Prolog kasutab Unix-i aknasüsteemi X11 värvinimesid), defineerime ka mõned värvid:
transf(X,Y,X1,Y1) :-
get(@graphics,width,W),
get(@graphics,height,H),
X1 is (W/2+X), Y1 is (H/2-Y).
transfAngle(Angle,Angle2) :-
AngleTemp is ((90-Angle) mod 360),
((AngleTemp>=0,!,Angle2=AngleTemp);Angle2 is AngleTemp+360).
transfAngleInv(Angle,Angle2) :-
Angle2 is ((90- Angle) mod 360).
rad(Kraad,Angle) :- Angle is (Kraad*pi/180).
kraad(AngleRad,Angle) :- Angle is AngleRad*180/pi.
Kujundite joonistamisel argumentideks sirglõigu pikkus ja arengustaadiumide arv. Ülalesitatud lumehelbe (neljanda arengustaadiumi järel) joonistab predikaat helve (enne selle peab käsuga draw olema loodud joonistamisaken):

helve(Pikkus,Tase) :-
penup, home,
setx(Pikkus/3),sety(-Pikkus/3),
setpencolor('#0000ff'),
pendown(Tase),
kylg(Pikkus,Tase),
left(120),
kylg(Pikkus,Tase),
left(120),
kylg(Pikkus,Tase).
kylg(Pikkus,0) :-
pendown(1),
forward(Pikkus).
kylg(Pikkus,Tase) :-
pendown(Tase),
UusPikkus is Pikkus / 3,
Uustase is Tase - 1,
kylg(UusPikkus,Uustase),
right(60),
kylg(UusPikkus,Uustase),
left(120),
kylg(UusPikkus,Uustase),
right(60),
kylg(UusPikkus,Uustase).
Teistsuguse lumeräitsaka loob predikaat helve1:

helve1(P,N) :-
home,
setpencolor('#0000ff'),
forward(P),
puu(P,N),
home,
right(120),
forward(P),
puu(P,N),
home,
left(120),
forward(P),
puu(P,N).
puu(Pikkus,0) :-
!,
forward(Pikkus).
puu(Pikkus,Tase) :-
getDraw(X,Y,A),
Uustase is Tase - 1,
UusPikkus is round(Pikkus*0.8),
right(60),
forward(Pikkus),
puu(UusPikkus,Uustase),
setDraw(X,Y,A),
left(60),
forward(Pikkus),
puu(UusPikkus,Uustase),
setDraw(X,Y,A),
forward(Pikkus),
puu(UusPikkus,Uustase).
Kasutades teisendusreeglit f → f,[,+,f,],f,f,[,-,f,], joonistades "vanemad" (varem genereeritud) oksad jämedama joonega ja lisades puu viimase taseme okste tippu õied, saame üsna loomutruu puukese:

oks(N,A) :-
clean,
penup,
home,
setpencolor('#00aa00'),
sety(-240),
pendown(N),
haar(N,A).
haar(0,_) :-
!,
forward(12),nupp(12,8).
haar(N,A) :-
forward(6*N),
getDraw(X,Y,Suund),
Nurk is 4-random(8)+A,
left(Nurk),
N1 is N - 1,
haar(N1,A),
penup,
setDraw(X,Y,Suund),
retractall(tase(_)),assert(tase(N)),
pendown(N),
forward(12*N),
getDraw(X1,Y1,Angle1),
Nurk1 is 4-random(8)+A,
right(Nurk1),
haar(N1,A),
penup,
setDraw(X1,Y1,Angle1),
pendown(N),
haar(N1,A).
nupp(Pikkus,Nurk) :-
setpencolor('#ffdd00'),
pendown(1),
forward(Pikkus),
back(Pikkus),
left(Nurk),
forward(Pikkus),
back(Pikkus),
left(Nurk),
forward(Pikkus),
back(Pikkus),
right((3*Nurk)),forward(Pikkus),
back(Pikkus),
right(Nurk),
forward(Pikkus),
back(Pikkus),
left((2*Nurk)),
setpencolor('#00aa00').
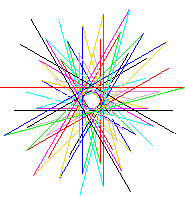

 :-numlist(1,6,List),L=60,N=60,home,penup,
:-numlist(1,6,List),L=60,N=60,home,penup,joonistab sümmeetriliselt joonistamisakna kespunkti (home) suhtes kõrvaltoodud kuusnurga.
Milliste predikaatidega saaks joonistada kõrvalolevad kujundid?
 ©2004
Jaak Henno
©2004
Jaak Henno