Wumpus on labürindis elav koletis, kes sööb igaühe, kes siseneb tema ruumi; keegi ei tea täpselt, kuidas ta välja näeb, kuid ta haiseb ja hais on tunda naaberruumis (kui ruumid on ühendatud). Mängija peab läbima labürindi, tapma Wumpuse (selleks on tal paar noolt) ja leidma labürindis peidetud kulla. Peale Wumpuse on labürindis veel teisigi ohte: kui ruumis on tuuletõmbus, siis on mõnes naaberruumis kuristik, kust enam välja ei pääse; mõnes ruumis on nahkhiired, kes lennutavad mängija mingisse juhuslikku (kuid mitte Wumpuse või kuristikuga) ruumi jne.
Vaatleme järgnevas mängu versiooni, kus labürint on täisnurkne K+1 x K+1 ruudustik (read ja veerud on indekseeritud 0,1,...,K); mängu algul on mängija ruudus [0,0] ja ta peab jõudma ruutu [K,K]. Et mäng oleks huvitavam, genereeritakse iga mängu algul uus labürint, kasutades selleks (veidi modifitseeritud) eelnevas esitatud labürindi genereerimise predikaati, mis töö lõpetamisel salvestab labürindi (s.t. kõik genereeritud läbipääsud) nimistus L :
tee_labyr([],_,L,L,K):-!,
retractall(labyr(_)),assert(labyr(L)),
retractall(dim(_)),assert(dim(K)).
tee_labyr(Käimata,Käidud,L1,L,K):-
vali_ruut(Käidud,Ruut,Ruut1,K),
delete(Käimata,Ruut1,Käimata1),
tee_labyr(Käimata1, [Ruut1|Käidud],[[Ruut,Ruut1]|L1],L,K).
vali_ruut(Käidud,Ruut,Ruut1,K):-
length(Käidud,P), findall(I,between(1,P,I),Indeksid),
vali_ruut1(Käidud,Ruut,Ruut1,K,Indeksid,P).
vali_ruut1(Käidud,Ruut,Ruut1,K,Indeksid,P):-
I is random(P), % 0 <= random(N) < N
((nth0(I,Käidud,Ruut),
naaber(Ruut,Ruut1,K),
not(member(Ruut1,Käidud))); %valik õnnestus
(delete(Indeksid,I,Indeksid1), %valik ei õnnestunud, kustutame vastva
indeksi ja proovime uuesti
P1 is P-1,P1>0,
vali_ruut1(Käidud,Ruut,Ruut1,K,Indeksid1,P1))).
pääseb(Ruum,Ruum1,Labyr):-
member([Ruum,Ruum1],Labyr);member([Ruum1,Ruum],Labyr).
naaber([N,M],[N1,M],K):-
N < K,
N1 is N+1.
naaber([N,M],[N,M1],K):-
M < K,
M1 is M+1.
naaber([N,M],[N1,M],_):-
N>0, N1 is N-1.
naaber([N,M],[N,M1],_):-
M>0, M1 is M-1.
naabrid(N,M,K,Naabrid):-
findall([N1,M1],naaber([N,M],[N1,M1],K),Naabrid).
yhendatud(N,M,Ruumid):-
labyr(L),
findall([N1,M1],pääseb([N,M],[N1,M1],L),Ruumid).
Kuna mängu- ja tekstiakna viita vajatakse mitmes predikaadis, defineerime need kohe mängu algul globaalmuutujatena (siis võib neid igal pool kasutada ja neid pole tarvis luua käsuga new); samuti kirjeldame assert- retract-lausetes kasutatavad predikaadid:
Et mängija ei peaks Prologi käsurida kasutama, genereerime mänguseisu näitava graafikaakna alla tekstiakna, milles Prolog annab infot mänguseisu kohta ja selle alla - käsurea, millelt mängija juhib mängu.
Predikaat mäng(K) loob graafilise mänguakna @aken, kus
näidatakse labürint
ja mängija praegune asukoht; mängija ülesande lihtsustamiseks näidatakse ka otsetee
algusest lõppu.
Selle alla tuleb tekstipaneel @tekst, kuhu kirjutatakse mängija asukoht ja praegune
liikumissuund (selle kõrgus ei ole pikselites, vaid tekstiridadena);
selle alla dialoogiaknasse @Command tuleb käsurida Input,
kust mängija juhib labürindis liikumist.
Käsureal kirjutatud käsk (selle lõppu ei tohi kirjutada punkti!) läheb Prologi
predikaadi run argumendiks, mis puhastab käsurea, teisendab sellelt loetud teksti (aatomi)
Prologi termiks ja käivitab selle siis Prologi süsteemipredikaadi call abil:
mäng(K):-
wumpus(400,500,K).
wumpus(W,H,K) :-
send(@aken,size(size(W,H))),
send(@aken,background(white)),
send(@tekst,editable(false)),
% HText is round(H/50),
send(@tekst,size(size(W,4))),
new(Input,text_item('?-','',message(@prolog,run,@arg1,@receiver))),
send(Input,length(W-100)),
new(@Command,dialog('CommandWindow')),
send(@Command,append(Input)),
send(@tekst,below,@aken),
send(@Command,below,@aken),
send(@Command,caret(Input)),
send(@aken,open),
init(W,H,K).
Info kasutajale info lisatakse (append) tekstiaknasse @tekst predikaadiga kirjuta; puhasta puhastab tekstiakna:
run(Tekst,Input) :-
send(Input,clear),
atom_to_term(Tekst,Clause,_),
call(Clause).
kirjuta(String) :-
send(@tekst,append(String)),send(@tekst,append('\n')).
kustuta :-
send(@tekst,clear).
Predikaat init loob labürindi ja joonistab selle aknasse:
init(Laius,Kõrgus,K):-
Kylg=16, %ruumi küljepikkus
retractall(kylg(_)),assert(kylg(Kylg)),
XC is Laius/2, %
YC is Kõrgus/2,
retractall(xC(_)),assert(xC(XC)),
retractall(yC(_)),assert(yC(YC)),
retractall(dim(_)),assert(dim(K)),
tee_labyr(L,K),
retractall(labür(_)),assert(labür(L)),
X0 is XC - Kylg*K/2,
Y0 is YC - Kylg*K/2,
joonista_labyr(L,Kylg,X0,Y0,K,0,0),
näita_tee(L,@aken,Kylg,X0,Y0,K),
paiguta_objektid(K), %see vajab teed!
send(@mängija,fill_pattern,colour(red)),
assert(olek(0,0,0,H,T)), %muidu järgnevas retract ebaõnnestub
kontrolli(0,0),
send(@aken,display,@mängija),
retractall(olek(_,_,_,_,_)),assert(olek(0,0,0,0,0)),
retractall(kulda(_)),assert(kulda(0)),
retractall(nooli(_)),assert(nooli(3)).
Objektide paigutamisel peab jälgima, et ükski kuristik ei tohi asuda algusest lõppu viival teel - kuna selliseid teid on vaid üks, ei oleks selline labürint üldse läbitav; algusest lõppu viiv tee (neid on üksainus!) on salvestatu predikaadiga tee(Tee). Wumpus võib teel olla - mängija pääseb edasi pärast Wumpuse tapmist; kulda ei või paigutada kuristikku (sealt ei saa seda kätte) ja algusruudus ei tohi olla midagi. Mitu sama tüüpi ruumi (auku või kulda sisaldavat) leiab rekursiivne predikaat leia_ruumid, mis oma esimese argumendi (auk või kuld) põhjal otsustab, kas käivitada suvalise ruumi leidmise predikaat juhuslik või mitte teel asuva ruumi leidmise predikaat mitte_teel:
paiguta_objektid(K):-
findall([N,M],(between(0,K,N),between(0,K,M)),Ruumid0),
delete(Ruumid0,[0,0],Ruumid),
juhuslik(Ruumid,[NW,MW]),
retractall(wumpus(_,_)),assert(wumpus(NW,MW)),
delete(Ruumid,[NW,MW],Ruumid1),
Auke is random(2)+1, %Auke = 1..3
Kulda is random(2)+1, %Kulda = 1..3
retractall(auk(_,_)),
leia_ruumid(auk,Ruumid1,Auke,Ruumid2),
leia_ruumid(kuld,Ruumid2,Kulda,_).
paiguta_wumpus(Ruumid,Ruum):-
juhuslik(Ruumid,Ruum).
mitte_teel(Ruumid,Ruum):-
tee(Tee),
subtract(Ruumid,Tee,Ruumid0),
juhuslik(Ruumid0,Ruum).
leia_ruumid(_,Ruumid,0,Ruumid):-!.
leia_ruumid(Mis,Ruumid,Mitu,Ruumid2):-
((Mis='auk',!,mitte_teel(Ruumid,[N,M]),assert(auk(N,M)));
(juhuslik(Ruumid,[N,M]),assert(kuld(N,M)))),
delete(Ruumid,[N,M],Ruumid1),
Mitu1 is Mitu - 1,
leia_ruumid(Mis,Ruumid1,Mitu1,Ruumid2).
juhuslik(Nimistu,Elem):-
length(Nimistu,Pikkus),
I is random(Pikkus),
nth0(I,Nimistu,Elem).
tuul(Naabrid,1):-
member([N,M],Naabrid),auk(N,M),!.
tuul(_,0).
hais(Naabrid,1):-
member([N,M],Naabrid),wumpus(N,M),!.
hais(_,0).
Labürindi joonistab ruum-ruumi järel ekraanile rekursiivne predikaatjoonista_labür, mis iga ruumi jaoks (selle kaks viimast argumenti on ruumi koordinaadid) laseb predikaatidel paremale, alla joonistada ruumi parema ja -alakülje - nii saadakse kõik labürindi ruumide vahelised seinad; kui kõik vaheseinad on joonistatud, joonistab predikaat kyljed labürindi välisküljed; predikaat näita_tee näitab loodud labyrindi läbipääsutee (see on vaid mängu silumiseks, mängus tuleks see välja kommenteerida):
joonista_labyr(_,Kylg,X0,Y0,K,K,K):-
kyljed(Kylg,X0, Y0,K),!.
joonista_labyr(L,Kylg,X0,Y0,K,N1,M1):-
% X0,Y0 - ylanurk!
N1<K,!, N2 is N1+1,
X is X0+N2*Kylg,
Y is Y0+M1*Kylg,
paremale(N1,N2,M1,L,X,Y,Kylg),
(M1<K,!,M2 is M1+1,X1 is X0+N1*Kylg,Y1 is Y+Kylg,alla(N1,M1,M2,L,X1,Y1,Kylg);true),
joonista_labyr(L,Kylg,X0,Y0,K,N2,M1).
joonista_labyr(L,Kylg,X0,Y0,K,N,M):-
M1 is M+1,
X is X0+K*Kylg,
Y is Y0+M1*Kylg,
alla(N,M,M1,L,X,Y,Kylg),
joonista_labyr(L,Kylg,X0,Y0,K,0,M1).
paremale(N1,N2,M,L,X,Y,Kylg):-
Y1 is Y+Kylg,
(
(pääseb([N1,M],[N2,M],L),!,
Y11 is Y+Kylg/3,Y12 is Y+2*Kylg/3,
send(@aken, display, new(_, line(X,Y,X,Y11,none))),
send(@aken, display, new(_, line(X,Y12,X,Y1,none))));
send(@aken, display, new(_, line(X,Y,X,Y1,none)))).
alla(N1,M1,M2,L,X,Y,Kylg):-
X1 is X+Kylg,
(
(pääseb([N1,M1],[N1,M2],L),!,
X11 is X+Kylg/3,X12 is X+2*Kylg/3,
send(@aken, display, new(_, line(X,Y,X11,Y,none))),
send(@aken, display, new(_, line(X12,Y,X1,Y,none))));
send(@aken, display, new(_, line(X,Y,X1,Y,none)))).
kyljed(Kylg,X0,Y0,K):-
X1 is X0+Kylg*(K+1),
%ylaY(Y0),
send(@aken, display, new(_, line(X0,Y0,X1,Y0,none))),
Y2 is Y0+Kylg*(K+1),
send(@aken, display, new(_, line(X0,Y2,X1,Y2,none))),
Y1 is Y0+Kylg,
send(@aken, display, new(_, line(X0,Y1,X0,Y2,none))),
Y11 is Y2-Kylg,
send(@aken, display, new(_, line(X1,Y0,X1,Y11,none))).
näita_tee([[[N1,M1],[N,N]]|L],P,Kylg,X0,Y0,N):- !,
hakka_joonistama([[[N1,M1],[N,N]]|L],[[N,N]],P,Kylg,X0,Y0,[[N,N]]). %viimane
- tee ruumid
näita_tee([_|L],P,Kylg,X0,Y0,N):-
näita_tee(L,P,Kylg,X0,Y0,N).
hakka_joonistama([],_,_,_,_,_,Tee):-!,
retractall(tee(_)),assert(tee(Tee)).
hakka_joonistama([[[N1,M1],[N2,M2]]|L],Käidud,P,Kylg,X0,Y0,Tee):-
member([N2,M2],Käidud),not(member([N1,M1],Käidud)),
!,
X1 is X0+N1*Kylg+Kylg/2,
X2 is X0+N2*Kylg+Kylg/2,
Y1 is Y0+M1*Kylg+Kylg/2,
Y2 is Y0+M2*Kylg+Kylg/2,
send(P, display, new(@Lne, line(X1,Y1,X2,Y2,none))),
send(@Lne,colour,colour(red)),
send(@Lne,pen,2),
hakka_joonistama(L,[[N1,M1]|Käidud],P,Kylg,X0,Y0,[[N1,M1]|Tee]).
hakka_joonistama([_|L],Käidud,P,Kylg,X0,Y0,Tee):-
hakka_joonistama(L,Käidud,P,Kylg,X0,Y0,Tee).
Mängija asukoha labürindis joonistab predikaat näita_mängija; pärast mängija joonistamist kirjutab ta tekstiaknasse mängija asukoha:
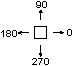Mängija asukoht on määratud ruumi koordinaatidega N,M (mängu algul on ta ruumis [0,0])
ja liikumissunaga Suund (selle tähendus vt. jooniselt); koos ruumis N,M olevate haisu ja tuulega on see info salvestatud
predikaadiga olek(N,M,Suund,Hais,Tuul).
Ta juhib labürindis liikumist käsurealt käskudega mine
(praeguses suunas järgmisse ruumi), pööra(Nurk)(Nurk = ±90, ±180, ±270); suhtelise suunamuutuse asemel
võib suuna anda ka väärtusena: suund(0), suund(90), suund(180),
suund(270); mängija võib ka küsida
praegust liikumissuunda käsuga suund(S); käsk
lase laseb noole praeguses suunas. Käskudega
uuesti ja uus_mäng(K) võib mängija kas alustada uuesti praeguse suurusega labürindis või
valida uue mängu jaoks teistsuguse suurusega labürindi:
mine:-
kirjuta('Ei pääse!').
mine(N,M,0):-
järgmine(N,M,0,N1,M),
kontrolli(N1,M). %kas ruumis on Wumpus või auk
mine(N,M,180):-
järgmine(N,M,180,N1,M),
kontrolli(N1,M).
mine(N,M,90):-
järgmine(N,M,90,N,M1),
kontrolli(N,M1).
mine(N,M,270):-
järgmine(N,M,270,N,M1),
kontrolli(N,M1).
järgmine(N,M,Suund,N1,M1):-
labür(L),
järgmine(N,M,Suund,N1,M1,L).
järgmine(N,M,0,N1,M,L):-
N1 is N+1,
pääseb([N,M],[N1,M],L).
järgmine(N,M,180,N1,M,L):-
N>0,
N1 is N-1,
pääseb([N,M],[N1,M],L).
järgmine(N,M,90,N,M1,L):-
M1 is M+1,
pääseb([N,M],[N,M1],L).
järgmine(N,M,270,N,M1,L):-
M>0,
M1 is M-1,
pääseb([N,M],[N,M1],L).
näita_suund:-
olek(_,_,Suund,_,_),
concat_atom(['Suund = ',Suund],Tekst),
kirjuta(Tekst).
suund(Suund):-
((var(Suund),!);
(retract(olek(N,M,_,H,T)),assert(olek(N,M,Suund,H,T)))),
näita_suund.
pööra(Nurk):-
retract(olek(N,M,Suund,H,T)),
Suund1 is (((3600 + Suund + Nurk) mod 360)//90)*90,
assert(olek(N,M,Suund1,H,T)),
näita_suund.
lase:-
retract(nooli(Nooli)),Nooli>0,!,
olek(N,M,Suund,_,_),
((järgmine(N,M,Suund,N1,M1),
wumpus(N1,M1),!,
kirjuta('Tapsid Wumpuse!'),
retractall(wumpus(_,_)));
kirjuta('Sein oli ees või ei olnud seal wumpust!')), %wumpus(N1,M1) ebaõnnestus!
Nooli1 is Nooli - 1,
assert(nooli(Nooli1)).
lase:-
kirjuta('Sul ei ole enam nooli!'). %Nooli>0 ebaõnnestus
uuesti:-
send(@aken,clear),
dim(K),
mäng(K).
uus_mäng(K):-
send(@aken,clear),
mäng(K).
Kogu mängu käiku kontrollib predikaat kontrolli(N,M), mis käivitub, kui mängija jõuab ruumi [N,M].
See predikaat peab (selles järjekorras):
- kontrollima, kas mängija on veel elus, s.t. ruumis ei ole kuristik ega Wumpus; kui on, teatab
sellest predikaat läbi
- (kui mängija jäi ellu) kindlaks tegema, kas ruumis on tuul või hais (selleks
leitakse kõigi ruumiga [N,M] ühendatud ruumide nimistu Naabrid);
- kontrollima, kas mängija leidis ruumis kulda; kui leidis, eemaldatakse kulla olemasolu kirjeldanud
lause kuld(N,M) (muidu mängija saaks siit taas kulda, kui ta teist korda tuleb ruumi)
- kui [N,M] on labürindi viimane ruum, siis kontrollima, kas Wumpus on tapetud ja kas mängija on
leidnud kulda; kui üks neist tingimustest pole täidetud, peab mängija jätkama.
Järgnevas on predikaat kontrolli esitatud paljude 'või'-de (;) abil väga kompaktselt, kuid sellest
aru saamiseks peab veidi pingutama; süsteemipredikaati retract on kasutatud nii
lause olek (eelneva ruumiga määratud olek) eemaldamiseks
kui ka oleku komponendi Suund lugemiseks
(see ei muutu järgmisse ruumi minnes); sellisel juhul ei või kasutada predikaati retractall.
läbi(Põhjus):-
kustuta,kirjuta('Mäng on läbi!'),send(@aken,clear),
((Põhjus = 'wumpus',!,kirjuta('Wumpus sööb sind!'),send(@aken,background(red)));
(kirjuta('Sa kukkusid kuristikku!'),send(@aken,background(black)))).
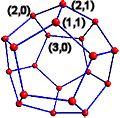Ken Thompsoni Wumpusejahi labürint ei olnud ristruudustik, vaid dodekaeeder.
Kuidas kirjeldada Wumpusejahti sellisel struktuuril! Dodekaeedri tippe võib
kirjeldada kahe koordinaadiga (kuid vastavalt peab muutma ka
mitmeid teisi predikaate), näiteks võib tippe esitada kolmel tasandil asuvatena
- joonisel meile kõige lähemal asuvad 5 tippu (esimene tasand), kõige kaugemal
asuvad viis tippu (kolmas tasand) ja nende vahel asuvad 10 tippu (keskmine
pole geomeetriliselt tasand, kuid see pole oluline); kui esimene koordinaat
T oleks tasand (T = 1,2,3) ja teine - tipu järjekorranumber tasandil, võiks
dodekaeedri tippe ( näiteks) esitada loeteluna (1,1),(1,3),(1,5),(1,7),(1,9),(3,0),
(3,2),(3,4),(3,6),(3,8),(2,0),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8),(2,9);
kaared oleks (näiteks) [(1,1),(1,3)],[(1,1),(2,1)],[(3,0),(3,8)],[(3,2),(2,2)]
jne.
©2004
Jaak Henno