Kuidas genereerida labürinti?

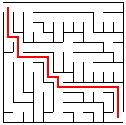
Paljud arvutimängud (Doom!) toimuvad labürindis, sellepärast vaaame, kuidas saab labürinti arvutis genereerida.

Labürinte on mitmesuguste omadustega; järgnevas teeme programmi labürindi genereerimiseks, mis:
- katab N x N ruudustiku; ridade/veergude ruudud on indekseeritud 0..N, sissepääs on ruudus [0,0] - väljapääs - ruudus [N,N];
- ei sisalda ligipääsmatuid ruute;
- labürindi igast ruudust pääseb igasse teise ruutu täpselt üht (korduvate ruutudeta) teed mööda (kahe viimase omadusega graafi nimetatakse kattepuuks).

Viimane omadus tagab, et sissepääsust [0,0] pääseb väljapääsu [N,N] parajasti üht (kordusteta) teed mööda.

Labürintide ja kattepuude genereerimiseks on esitatud palju algoritme, vaatleme järgnevas üht lihtsamatest, nn käikude uuristamise algoritmi:
- lisame igal sammul juba moodustatud labürindile (genereerimist alustades sisaldab labürint vaid ruudu [0,0]) ruudu, millesse pääseb mingist juba moodustatud labürindiosa ruudust, kuid mis ise labürinti veel ei kuulu; jätkame, kuni kõik ruudustiku ruudud on lisatud labürindile.

On selge, et selline algoritm annab silmusteta labürindi, mis katab kõiki ruute, s.t. kattepuu.

Labürindi moodustamiseks kogume algul süsteemipredikaadiga findall kõik ruudud [X,Y] (0 <= X <= N) Käimata ruutude nimistuks ja eemaldame sealt ruudu [0,0], millest saab juba labürinti kuuluvate ruutude nimistu Käidud; labürindi kirjelduse saame nimistuna L kaarte paaridest [Ruut, Ruut1], kus Ruut on sellel sammul valitud juba labürinti kuuluv ruut ja Ruut1 - mingi tema naabruses (kõrval või üleval või all) olev ruut, mis seni labürinti veel ei kuulunud; eemaldame ruudu Ruut1 käimata ruutude nimistust ja jätkame, kuni käimata ruutude nimistu on tühi:

tee_labyr(L,N):-
findall([X,Y],(between(0,N,X),between(0,N,Y)),Käimata0),
delete(Käimata0,[0,0],Käimata),
tee_labyr(Käimata,[[0,0]],[],L,N).

tee_labyr([],_,L,L,_):-!.

tee_labyr(Käimata,Käidud,L1,L,N):-
vali_ruut(Käidud,Ruut,Ruut1,N),
delete(Käimata,Ruut1,Käimata1),
tee_labyr(Käimata1, [Ruut1|Käidud],[[Ruut,Ruut1]|L1],L,N).

Et labürint tuleks võimalikult ühtlane, ilma pikkade otseteedeta, valime igal sammul võimalikult juhuslikult juba labürinti kuuluva ruudu, mille naabrusest hakkame otsima labürinti mittekuuluvat ruutu. Kuna selle ruudu valik võib ka ebaõnnestuda (valitud ruudu naabruses kuuluvad juba kõik ruudud labürinti), peab valikuprotseduur andma tagurdamisel erineva ruudu. Kahjuks annab Swi-Prologi sisseehitatud protseduur random ka tagurdamisel sama arvu, sellepärast ei kõlba sirgjooneline lahendus (Swi-Prologi sisseehitatud protseduur nth1(I, Nimistu, Element) valib nimistust Nimistu I-nda elemendi Element, kusjuures nimistu elementide indeksid algavad 1-st; kui indeksid algavad 0-st, peab kasutama protseduuri nth0):

vali_ruut1(Käidud,Ruut,Ruut1,N):-
length(Käidud,P),
I is (random(P)+1),
nth1(I,Käidud,Ruut),
naaber(Ruut,Ruut1,N),
not(member(Ruut1,Käidud)).

Sellepärast peab uue ruudu valikul veidi nipitama: moodustame nimistu veel käimata ruutude nimistu indeksitest ja eemaldame sealt iga kord juba testitud indeksi; niimoodi saadakse tagurdamisel kindlasti alati uus ruut:

vali_ruut(Käidud,Ruut,Ruut1,N):-
length(Käidud,P), findall(I,between(1,P,I),Indeksid),
vali_ruut1(Käidud,Ruut,Ruut1,N,Indeksid,P).

vali_ruut1(Käidud,Ruut,Ruut1,N,Indeksid,P):-
I is (random(P)+1), % 0 <= random(N) < N
((nth1(I,Käidud,Ruut),
naaber(Ruut,Ruut1,N),
not(member(Ruut1,Käidud)));
(delete(Indeksid,I,Indeksid1),P1 is P-1,P1>0,vali_ruut1(Käidud,Ruut,Ruut1,N,Indeksid1,P1))).

Predikaat naaber annab kõik ruudu Ruut naabruses (kõrval, all või üleval) olevad ruudud; kuna labürindi serval ei ole naabreid kõigis suundades, peab ta teadma ka labürindi dimensiooni N:
naaber([X,Y],[X1,Y],N):-
X < N,
X1 is X+1.

naaber([X,Y],[X,Y1],N):-
Y < N,
Y1 is Y+1.

naaber([X,Y],[X1,Y],_):-
X>0, X1 is X-1.

naaber([X,Y],[X,Y1],_):-
Y>0, Y1 is Y-1.

Labürindi ekraanile joonistamine on XPCE graafikaprotseduuride abil lihtne; protseduur joonista(N)kontrollib algul, kas graafikaaken on juba loodud ja võimaldab seega samasse aknasse genereerida erinevaid labürinte; pärast labürindi konstrueerimist predikaadiga tee_labür joonistab protseduur joonista_labür selle ekraanile ja protseduur näita_tee joonistab (punasega) silmusteta tee algusruudust [0,0] lõppruuduni [N,N]:
joonista(N):-
Kõrgus=400,
Laius=600,
((clause(aken(P),true),!,send(P,clear));
(new(F, frame('Labyrint')),
send(F, append,
new(P, picture('Labyrint', size(Laius,Kõrgus)))),
send(P, open),
retractall(aken(_)),
assert(aken(P)))),
Kylg=10, %ruumi!
X0 is Laius/2-Kylg*N/2,
Y0 is Kõrgus/2-Kylg*N/2,
kyljed(Kylg,X0, Y0,N,P),
tee_labyr(L,N),
joonista_labyr(L,P,Kylg,X0,Y0,N,0,0),
näita_tee(L,P,Kylg,X0,Y0,N).

Labürindi joonistamisel läbitakse kõik ruudud rida-realt; igas ruudus [N1,M1] kontrollitakse, kas selle parempoolne serv ja selle alumine serv on kinni (tuleb joonistada sirglõik); rea viimases ruudus paremale loomulikult pole enam midagi tarvis joonistada ja viimases peas pole alla enam midagi joonistada; töö lõpeb, kui rea- ja veeruindeksid N1,M1 on mõlemad võrdsed N-ga:

joonista_labyr(_,_,_,_,_,N,N,N):-!.

joonista_labyr(L,P,Kylg,X0,Y0,N,N1,M1):-
N1<N,!, N2 is N1+1,
paremale(N1,N2,M1,L,P,X0,Y0,Kylg),
(M1<N,!,M2 is M1+1,alla(N1,M1,M2,L,P,X0,Y0,Kylg);true),
joonista_labyr(L,P,Kylg,X0,Y0,N,N2,M1).

joonista_labyr(L,P,Kylg,X0,Y0,N,N,M):-
M1 is M+1,
alla(N,M,M1,L,P,X0,Y0,Kylg),
joonista_labyr(L,P,Kylg,X0,Y0,N,0,M1).

paremale(N1,N2,M,L,P,X0,Y0,Kylg):-
not(member([[N1,M],[N2,M]],L)),
not(member([[N2,M],[N1,M]],L)),
X is X0+N2*Kylg,
Y1 is Y0+M*Kylg,
Y2 is Y1+Kylg,
send(P, display, new(_, line(X,Y1,X,Y2,none)));true.

alla(N1,M1,M2,L,P,X0,Y0,Kylg):-
not(member([[N1,M1],[N1,M2]],L)),
not(member([[N1,M2],[N1,M1]],L)),
X1 is X0+N1*Kylg,
X2 is X1+Kylg,
Y is Y0+(M1+1)*Kylg,
send(P, display, new(_, line(X1,Y,X2,Y,none)));true.

kyljed(Kylg,X0,Y0,N,P):-
%ylaX(X0),
X1 is X0+Kylg*(N+1),
%ylaY(Y0),
send(P, display, new(_, line(X0,Y0,X1,Y0,none))),
Y2 is Y0+Kylg*(N+1),
send(P, display, new(_, line(X0,Y2,X1,Y2,none))),
Y1 is Y0+Kylg,
send(P, display, new(_, line(X0,Y1,X0,Y2,none))),
Y11 is Y2-Kylg,
send(P, display, new(_, line(X1,Y0,X1,Y11,none))).

Algusruudust [0,0] lõppruutu [N,N] viiva silmusteta tee joonistamisel saab ära kasutada, et nimistusse L lisati ruudupaarid [Ruut, Ruut1] alati nii, et teisena on just lisatud ruut Ruut1, seega jõutakse lõppruuduni mingi paariga [[N1,M1],[N,N]]; kõik paarid, mis on lisatud veel pärast seda, võib kohe kõrvale jätta (nad ei saa kuuluda algusest lõppu viivalel kordusteta teele):

näita_tee([[[N1,M1],[N,N]]|L],P,Kylg,X0,Y0,N):- !,
hakka_joonistama([[[N1,M1],[N,N]]|L],[[N,N]],P,Kylg,X0,Y0).

näita_tee([_|L],P,Kylg,X0,Y0,N):-
näita_tee(L,P,Kylg,X0,Y0,N).

hakka_joonistama([],_,_,_,_,_):-!.
hakka_joonistama([[[N1,M1],[N2,M2]]|L],Käidud,P,Kylg,X0,Y0):-
member([N2,M2],Käidud),not(member([N1,M1],Käidud)),
!,
X1 is X0+N1*Kylg+Kylg/2,
X2 is X0+N2*Kylg+Kylg/2,
Y1 is Y0+M1*Kylg+Kylg/2,
Y2 is Y0+M2*Kylg+Kylg/2,
send(P, display, new(@Lne, line(X1,Y1,X2,Y2,none))),
send(@Lne,colour,colour(red)),
send(@Lne,pen,2),
hakka_joonistama(L,[[N1,M1]|Käidud],P,Kylg,X0,Y0).
hakka_joonistama([_|L],Käidud,P,Kylg,X0,Y0):-
hakka_joonistama(L,Käidud,P,Kylg,X0,Y0).

Ülesandeid:
1. Ylesande tekst

Küsimused, probleemid: ©2004 Jaak Henno