Chomsky klassifikatsioon

Produktsioonide kuju põhjal liigitas kanada lingvist, matemaatik ja filosoof Chomsky grammatikad nelja klassi.
  • 0-tyypi (e. rekursiivselt loenduvate) grammatikate produktsioonidele kitsendusi ei ole.
  • 1-tüüpi (e. kontekstitundlike) grammatikate kõik produktsioonid peavad olema kujul
    w1Xw2 w1vw2
    kus X on mitteterminal, w1, w2, v - suvalised sõnad mis võivad sisaldada nii terminale kui ka mitteterminale ja v ei ole tühi (s.t. mitteterminali X asendamine sõnaga v on lubatud vaid kontekstis w1.. w2); erandina on lubatud produktsioon Xo ( - tühi sõna), kui algussümbol Xo ei esine ühegi produktsiooni paremal pool.
    Saab näidata, et iga selle klassi grammatika poolt kirjeldatud keelt võib esitada ka nn. pikkust suurendava grammatikaga, st. grammatikaga, mille kõik produktsioonid w w' rahuldavad tingimust |w| 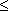|w'|
  • 2-tüüpi e. kontekstivabade grammatikate kõik produktsioonid peavad olema kujul X v, kus X on mitteterminal;
  • 3-tüüpi e. regulaarsete grammatikate kõik produktsioonid peavad olema kujul
    X Ya
    või
    X a
    kus X,Y on mitteterminalid ja a - terminal.

    Saab näidata, et regulaarsete grammatikate poolt genereeritud keeled saab kirjeldada ka grammatikatega, mille produktsioonid on parempoolsed, s.t. kujul
    X aY või X a

    Selles klassifikatsioonis iga järgmine klass kuulub eelmisesse (s.t. näiteks regulaarsed grammatikad rahuldavad kõiki kontekstivabade grammatikate klassi nõudeid), selleärast laieneb Chomsky klassifikatsioon loomulikul viisil ka keeltele: keelt nimetatakse klassi i (i=3,2,1,0 ) keeleks ehk vastavalt regulaarseks, kontekstivabaks, kontekstitundlikuks, rekursiivselt loenduvaks, kui teda saab genereerida klassi i grammatikaga ja ei saa genereerida klassi i+1 (s.t. rangema, kitsama klassi) grammatikaga.

    Vaatamata liigituse formaalsele alusele (produktsioonide kuju) on Chomsky klassifikatsioonil sügav sisu. Paljud keelte käsitlemisel olulised omadused, näiteks keeli tunnistava programmi töökiirus ja mäluvajadus jne on seda paremad, mida lihtsama klassi keeli vaadeldakse. Sellepärast püütakse translaatorite alametappidel (leksiline analüüs, süntaksi analüüs jne) kasutada keeli, mis on kas regulaarsed või kontekstivabad. See võimaldab vastava etapi kirjeldada lähteteksti ühekordse vasakult-paremale läbivaatamisena, kusjuures ajaduse korral vaatatakse enne mingi teisenduse tegemist käsitletavast sümbolist ka paar eespool tulevat sümbolit (nn look-ahead) ja seega sooritada vastava etappi (peaaegu) lineaarse kiirusega, s.t. nii, et programmi töötaktide arv on võrdeline sisendteksti pikkusega.

    Ülesandeid:

    1. Millisesse klassi kuulusid eespool vaadeldud eesti keele lihtlause ja lihtsa programmeerimiskeele süntaksi kirjeldused?

    Küsimused, probleemid:
    jaak@cc.ttu.ee

    Tagasi loengute sisukorra juurde