Regulaarsed keeled, regulaarsed avaldised ja lõplikud automaadid

Regulaarsed keeled on keeled, mida saab genereerida regulaarse e. klass-3 grammatikaga (Chomsky klassifikatsioon), s.t. grammatikaga (A,V,X_o,P), mille köik produktsioonid on kujul
X Ya või
X a
kus X,Y V ja a A.
Grammatika on formalism keelte (s.t. kõigi keelde kuuluvate sõnade) genereerimiseks. See on ka tavaliselt inimese jaoks väga hästimõistetav viis keelte defineerimiseks. Genereerimismehhanismi olemasolu aga ei taga veel, et suvalise söna w ja (grammatika abil esitatud) keele L jaoks oleks alati selge, kuidas lahendada probleemi: kas sõna w kuulub keelde L, s.t. w ^? L

Söna keelde kuuluvuse probleemi (aga seda peab arvuti lahendama igas keele teisendusprogrammis, s.t. kõigil transleerimise etappidel) kasutatakse automaate. Igale grammatikate klassile Chomsky klassifikatsioonis vastab oma automaatide klass.

Regulaarseid keeli saab defineerida ka kui keeli, mida saab tunnistada lõpliku automaadiga.

Löplik automaat on viisik (A, S, s_o, F, P), kus
A on sisendtähestik (terminalide tähestik)
S on olekute hulk (lõplik)
s_o S on algolek
F S on lõppolekute hulk
P on automaadi üleminekuid (tööd) kirjeldavate produktsioonide hulk. Produktsiooni sa s' semantika (tähendus) on, et kui automaat olekus s loeb sisendlindilt sümboli (sisendtähestiku tähe) a, läheb ta olekusse s' .
Löplikke automaate esitatakse sageli nende graafiga. Automaadi graafi tippudeks on olekud, kaarteks - üleminekud, kaart tähistatakse sisendsümboliga, mis vastava ülemineku esile kutsub.

Regulaarseid keeli saab esitada ka nn regulaarsete avaldistega. Regulaarsed avaldised (ja regulaarsele avaldisele e vastav keel L(e), s.t. sõnade hulga terminalide tähestikus T) defineeritakse rekursiivselt:

on regulaarne avaldis, L(

) =

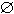; (s.t. tühjale sõnale vastab tühi keel)

iga x

T on regulaarne avaldis, L(x) = {x} (s.t. vastav keel koosneb ühest ühetähelisest sõnast);

kui e₁,e₂,...,e_n on regulaarsed avaldised (ja neile vastavad keeled L(e₁),L(e₂),...,L(e_n) ), siis ka:

1. (e₁ | e₂ | ... | e_n ) on regulaarne avaldis ja L((e₁ | e₂ | ... | e_n )) =

L(e_i);

2. e₁e₂...e_n on regulaarne avaldis ja sellele vastab keel L(e₁e₂...e_n ) = L(e₁)L(e₂)...L(e_n) (s.t. kõikvõimalikud n teguri korrutised, kus i-s tegur on keelest L(e_i), i=1...n )

3. eⁿ on regulaarne avaldis, eⁿ = ee...e (n tegurit)

4. e^* on regulaarne avaldis ja L(e^*) =

L(eⁱ), i = 0,1,2,..., s.t. L(e^*) =

L(e)

L(e²)

...

Näide 1. Grammatika ({0,1,=}, {X_o, Y, Y₁}, X_o, {X_o Y = Y, Y | Y0 | Y₁1, Y₁ Y₁0 | Y1}
genereerib keele { w₁ = w₂ | | w₁|₁ = |w₂|₁ mod 2}, s.t. kõik jadad w₁ = w₂, kus sõnades w₁, w₂ on sümbolite "1" esinemiste arv sama paarsusega, s.t. kas mõlemates paaris või mõlemates paaritu arv. Selle keele tunnistab automaat

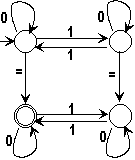
(automaadi algolek märgitakse graafil sellesse olekusse suubuva noolena; lõppolek - kahekorse ringiga)

ÜÜlesandeid: 1. Ülaltoodud grammatika genereerib regulaarse keele (sest selle keele tunnistab esitatud lõplik automaat), kuid ei ole ise regulaarne (produktsioon X_o

Y = Y ei ole regulaarse grammatika produktsioon). Leia selle keele jaoks regulaarne grammatika.

2. Lülitusskeemis kaks lülitit juhivad sama pirni - vajutus lüliti üleval olevale otsale muudab pirni oleku (põleb, ei) vastupidiseks. Sisendsignaalideks (terminalideks) on v₁, p₁ , v₂, p₂ (vajutused 1. või 2. lüliti vasak- ja parempoolsele otsale); algolekus on mõlema lüliti parempoolne ots üleval ja pirn ei põle. Keel koosneb kõikvõimalöikest terminalide v₁, p₁ , v₂, p₂ jadadest, mis panevad pirni põlema (vajutused vöivad olla suvalises järjekorras lüliti olekust sõltumata), näiteks p₁, p₂, p₁p₁, p₁p₂v₂, p₁v₁v₂p₂, v₁v₂p₂ jne. Leia regulaarne grammatika ja lõplik automaat selle keele genereerimiseks/tunnistamiseks.

Küsimused, probleemid:

jaak@cc.ttu.ee

Tagasi loengute sisukorra juurde