Näide2: Reaalarve kirjeldav regulaarne grammatika ja automaat

Reaalarvud on erikujulised, s.t. oma vormi (süntaksiga) määratud märkide jadad (stringid); käesolevas näites reaalarv:
- peab sisaldama järgusümbolit 10 ja selle järel mingit täisarvu (märgiga või ilma)
- kümnendosa eraldajaks on punkt .
- arv võib alata punktiga (täisosa puudub) ja punkt võib üldse puududa (arv algab järguga), kuid kui punkt on, peab sellele järgnema vähemalt üks number (enne järku).
Neid (suntaksi)nõudeid rahuldavate reaalarvude näideteks oleks:
3.1710+3
5.410-7
.3103
10-5

kuid näiteks .10+5 ja 3.14 ei ole (korrektselt kirjutatud) reaalarvud.

Reaalarvude kirjutamisel võib kasutada järgmisi sümboleid, s.t. reaalarvude terminalide tähestik on:
VT = {0,1,2,3,4,5,6,7,8,9,.,10,+,-}

Mitteterminalid (abimõisted) oleksid
VN = {REAL_NUMB, INT, DIG, START_PART, END_PART, SIGN}

ja produktsioonid:
DIG 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
INT DIG | INT DIG
-- st täisarv peab sisaldama vähemalt ühe numbri; regulaarse avaldise abil võib viimast produktsiooni kirjutada ka lühemalt:
INT DIG+ (= DIG DIG *) = (0|1|...|9)+ )

START_PART INT . INT 10 | 10 | . INT 10 | INT . 10
END_PART SIGN INT | INT
SIGN + | -
REAL_NUMB START_PART END_PART

Sellest grammatikast on lihtne saada reaalarve kirjeldav regulaarne avaldis:

REAL_NUM START_PART END_PART
( DIG+ . DIG+ 10 | 10 | . DIG+ 10 | DIG+ . 10 ) ( (+ | -) DIG+ | DIG+ )
( DIG+ . DIG+ 10 | 10 | . DIG+ 10 | DIG+ . 10 ) ( (+ | -) DIG+ | DIG+ )

Selle süntaksi tunnistab automaat


Ülesandeid:

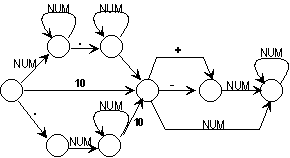
Koosta ADA-programm, mis tunnistab reaalarve vastavalt ülaltoodud reaalarvu süntaksi kirjeldusele (vt Pico-Algol programme tunnistavat programmi!)

Küsimused, probleemid:
jaak@cc.ttu.ee

Tagasi loengute sisukorra juurde